题目内容
已知一组正数x1,x2,x3,x4的方差为S2= (x12+x22+x32+x42-16),则数据x1+2,x2+2,BN的平均数为( )
(x12+x22+x32+x42-16),则数据x1+2,x2+2,BN的平均数为( )A.2
B.4
C.-2
D.不确定
【答案】分析:根据方差的公式求得原数据的平均数后,求得新数据的平均数即可.
解答:解:由方差的计算公式可得:
S12=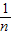 [(x1-
[(x1-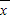 )2+(x2-
)2+(x2-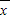 )2+…+(xn-
)2+…+(xn-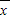 )2]
)2]
=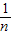 [x12+x22+…+xn2-2(x1+x2+…+xn)•
[x12+x22+…+xn2-2(x1+x2+…+xn)•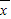 +n
+n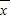 2]
2]
=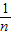 [x12+x22+…+xn2-2n
[x12+x22+…+xn2-2n 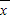 2+n
2+n 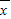 2]
2]
=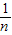 [x12+x22+…+xn2]-
[x12+x22+…+xn2]-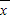 2=
2= (x12+x22+x32+x42-16),
(x12+x22+x32+x42-16),
可得平均数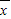 1=2.
1=2.
对于数据x1+2,x2+2,x3+2,x4+2,x5+2,有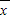 2=2+2=4,
2=2+2=4,
故选B.
点评:此题主要考查了方差和平均数的性质,一般地设有n个数据,x1,x2,…xn,若每个数据都放大或缩小相同的倍数后再同加或同减去一个数,其平均数也有相对应的变化,方差则变为这个倍数的平方倍.
解答:解:由方差的计算公式可得:
S12=
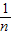 [(x1-
[(x1-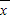 )2+(x2-
)2+(x2-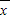 )2+…+(xn-
)2+…+(xn-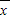 )2]
)2]=
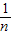 [x12+x22+…+xn2-2(x1+x2+…+xn)•
[x12+x22+…+xn2-2(x1+x2+…+xn)•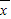 +n
+n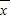 2]
2]=
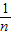 [x12+x22+…+xn2-2n
[x12+x22+…+xn2-2n 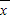 2+n
2+n 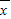 2]
2]=
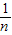 [x12+x22+…+xn2]-
[x12+x22+…+xn2]-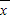 2=
2= (x12+x22+x32+x42-16),
(x12+x22+x32+x42-16),可得平均数
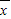 1=2.
1=2.对于数据x1+2,x2+2,x3+2,x4+2,x5+2,有
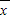 2=2+2=4,
2=2+2=4,故选B.
点评:此题主要考查了方差和平均数的性质,一般地设有n个数据,x1,x2,…xn,若每个数据都放大或缩小相同的倍数后再同加或同减去一个数,其平均数也有相对应的变化,方差则变为这个倍数的平方倍.

练习册系列答案
相关题目