题目内容
已知函数f(x)=msinx+ncosx,且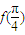 是它的最大值,(其中m、n为常数且mn≠0)给出下列命题:
是它的最大值,(其中m、n为常数且mn≠0)给出下列命题:①
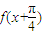 是偶函数;
是偶函数;②函数f(x)的图象关于点
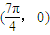 对称;
对称;③
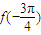 是函数f(x)的最小值;
是函数f(x)的最小值;④记函数f(x)的图象在y轴右侧与直线
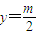 的交点按横坐标从小到大依次记为P1,P2,P3,P4,…,则|P2P4|=π
的交点按横坐标从小到大依次记为P1,P2,P3,P4,…,则|P2P4|=π⑤
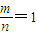 .
.其中真命题的是 (写出所有正确命题的编号)
【答案】分析:由题意可得f(x)=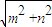 sin(x+
sin(x+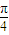 ),对于①,由于
),对于①,由于 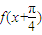 =cosx,是偶函数,故①正确.
=cosx,是偶函数,故①正确.
对于②,由于当x=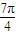 时,f(x)=0,故②正确.
时,f(x)=0,故②正确.
对于③,由于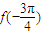 =-
=- ,是 函数f(x)的最小值,故 ③正确.
,是 函数f(x)的最小值,故 ③正确.
对于④,由题意可得,|P2P4|等于一个周期2π,故 ④不正确.
对于⑤,由tan∅=tan(2kπ+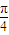 )=
)=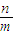 =1,可得⑤正确.
=1,可得⑤正确.
解答:解:由于函数f(x)=msinx+ncosx=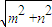 sin(x+∅),且
sin(x+∅),且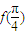 是它的最大值,
是它的最大值,
∴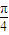 +∅=2kπ+
+∅=2kπ+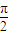 ,k∈z,∴∅=2kπ+
,k∈z,∴∅=2kπ+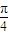 ,∴tan∅=
,∴tan∅=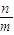 =1.
=1.
∴f(x)=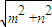 sin(x+2kπ+
sin(x+2kπ+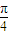 )=
)=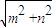 sin(x+
sin(x+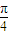 ).
).
对于①,由于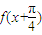 =
=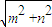 sin(x+
sin(x+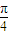 +
+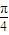 )=cosx,是偶函数,故①正确.
)=cosx,是偶函数,故①正确.
对于②,由于当x=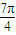 时,f(x)=0,故函数f(x)的图象关于点
时,f(x)=0,故函数f(x)的图象关于点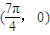 对称,故②正确.
对称,故②正确.
对于③,由于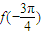 =
=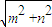 sin(-
sin(- )=-
)=-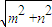 ,是 函数f(x)的最小值,故 ③正确.
,是 函数f(x)的最小值,故 ③正确.
对于④,函数f(x)的图象即把函数 y=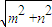 sinx的图象向左平移
sinx的图象向左平移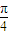 个单位得到的,故|P2P4|等于
个单位得到的,故|P2P4|等于
一个周期2π,故 ④不正确.
对于⑤,由tan∅=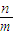 =1,可得⑤正确.
=1,可得⑤正确.
故答案为:①②③⑤.
点评:本题考查两角和正弦公式,正弦函数的最值,对称性,奇偶性,函数图象的变换,得到 f(x)=
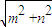 sin(x+
sin(x+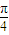 ),是解题的关键.
),是解题的关键.
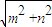 sin(x+
sin(x+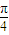 ),对于①,由于
),对于①,由于 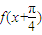 =cosx,是偶函数,故①正确.
=cosx,是偶函数,故①正确.对于②,由于当x=
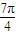 时,f(x)=0,故②正确.
时,f(x)=0,故②正确.对于③,由于
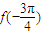 =-
=-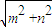 ,是 函数f(x)的最小值,故 ③正确.
,是 函数f(x)的最小值,故 ③正确.对于④,由题意可得,|P2P4|等于一个周期2π,故 ④不正确.
对于⑤,由tan∅=tan(2kπ+
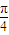 )=
)=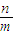 =1,可得⑤正确.
=1,可得⑤正确.解答:解:由于函数f(x)=msinx+ncosx=
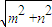 sin(x+∅),且
sin(x+∅),且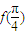 是它的最大值,
是它的最大值,∴
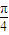 +∅=2kπ+
+∅=2kπ+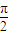 ,k∈z,∴∅=2kπ+
,k∈z,∴∅=2kπ+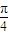 ,∴tan∅=
,∴tan∅=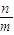 =1.
=1.∴f(x)=
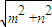 sin(x+2kπ+
sin(x+2kπ+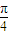 )=
)=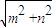 sin(x+
sin(x+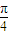 ).
).对于①,由于
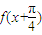 =
=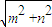 sin(x+
sin(x+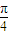 +
+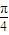 )=cosx,是偶函数,故①正确.
)=cosx,是偶函数,故①正确.对于②,由于当x=
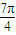 时,f(x)=0,故函数f(x)的图象关于点
时,f(x)=0,故函数f(x)的图象关于点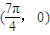 对称,故②正确.
对称,故②正确.对于③,由于
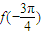 =
=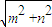 sin(-
sin(- )=-
)=-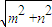 ,是 函数f(x)的最小值,故 ③正确.
,是 函数f(x)的最小值,故 ③正确.对于④,函数f(x)的图象即把函数 y=
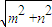 sinx的图象向左平移
sinx的图象向左平移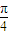 个单位得到的,故|P2P4|等于
个单位得到的,故|P2P4|等于一个周期2π,故 ④不正确.
对于⑤,由tan∅=
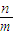 =1,可得⑤正确.
=1,可得⑤正确.故答案为:①②③⑤.
点评:本题考查两角和正弦公式,正弦函数的最值,对称性,奇偶性,函数图象的变换,得到 f(x)=
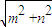 sin(x+
sin(x+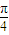 ),是解题的关键.
),是解题的关键. 
练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目