题目内容
直线l过点M(-1,2)且与以P(-2,-3),Q(4,0)为端点的线段PQ相交,则l的斜率的取值范围是( )
A、[-
| ||||||
B、[-
| ||||||
C、[-
| ||||||
D、(-∞,-
|
分析:画出图形,由题意得 所求直线l的斜率k满足 k≥kPB 或 k≤kPA,用直线的斜率公式求出kPB 和kPA 的值,
解不等式求出直线l的斜率k的取值范围.
解不等式求出直线l的斜率k的取值范围.
解答: 解:如图所示:M(-1,2)且与以P(-2,-3),Q(4,0),
解:如图所示:M(-1,2)且与以P(-2,-3),Q(4,0),
由题意得,所求直线l的斜率k满足kPM≤k或k≤kMQ,
即 kPM≥
=5,kMQ≤
=-
,
∴k∈(-∞,-
]∪[5,+∞),
故选:D.
 解:如图所示:M(-1,2)且与以P(-2,-3),Q(4,0),
解:如图所示:M(-1,2)且与以P(-2,-3),Q(4,0),由题意得,所求直线l的斜率k满足kPM≤k或k≤kMQ,
即 kPM≥
| 2+3 |
| -1+2 |
| 0-2 |
| 4+1 |
| 2 |
| 5 |
∴k∈(-∞,-
| 2 |
| 5 |
故选:D.
点评:本题考查恒过定点的直线系以及直线的斜率公式的应用,体现了数形结合的数学思想.

练习册系列答案
相关题目
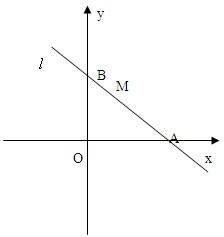 已知直线l过点M(1,2),且直线l与x轴正半轴和y轴的正半轴交点分别是A、B,(如图,注意直线l与坐标轴的交点都在正半轴上)
已知直线l过点M(1,2),且直线l与x轴正半轴和y轴的正半轴交点分别是A、B,(如图,注意直线l与坐标轴的交点都在正半轴上) 已知点Q(x,y)位于直线x=-3右侧,且到点F(-1,0)与到直线x=-3的距离之和等于4.
已知点Q(x,y)位于直线x=-3右侧,且到点F(-1,0)与到直线x=-3的距离之和等于4.