题目内容
设函数f(x)=msinx+cosx(x∈R)的图象经过点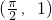 .
.
(Ⅰ)求y=f(x)的解析式,并求函数的最小正周期和单调递增区间
(Ⅱ)若 ,其中A是面积为
,其中A是面积为 的锐角△ABC的内角,且AB=2,求AC和BC的长.
的锐角△ABC的内角,且AB=2,求AC和BC的长.
解:(Ⅰ)∵函数f(x)=msinx+cosx(x∈R)的图象经过点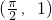
∴ ,∴m=1,∴
,∴m=1,∴ ,∴函数的最小正周期T=2π
,∴函数的最小正周期T=2π
由 可得
可得 ,
,
∴y=f(x)的调递增区间为 .
.
(Ⅱ)因为 即
即 ,
,
∴ ,
,
∵A是面积为 的锐角△ABC的内角,∴
的锐角△ABC的内角,∴ ,
,
∵ ∴AC=3
∴AC=3
由余弦定理得:BC2=AC2+AB2-2•AB•ACcosA=7
分析:(Ⅰ)函数f(x)=msinx+cosx(x∈R)的图象经过点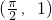 ,求出m,利用两角和的正弦函数化为一个角的一个三角函数的形式,即可得到函数的解析式,然后求出周期和单调增区间.
,求出m,利用两角和的正弦函数化为一个角的一个三角函数的形式,即可得到函数的解析式,然后求出周期和单调增区间.
(Ⅱ)利用 ,求出sinA,l利用面积为
,求出sinA,l利用面积为 ,AB=2,求AC,余弦定理求出BC的长.
,AB=2,求AC,余弦定理求出BC的长.
点评:本题是基础题,考查三角函数的正确、单调性、余弦定理的应用,考查计算能力,常考题型.
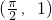
∴
 ,∴m=1,∴
,∴m=1,∴ ,∴函数的最小正周期T=2π
,∴函数的最小正周期T=2π由
 可得
可得 ,
,∴y=f(x)的调递增区间为
 .
.(Ⅱ)因为
 即
即 ,
,∴
 ,
,∵A是面积为
 的锐角△ABC的内角,∴
的锐角△ABC的内角,∴ ,
,∵
 ∴AC=3
∴AC=3由余弦定理得:BC2=AC2+AB2-2•AB•ACcosA=7
分析:(Ⅰ)函数f(x)=msinx+cosx(x∈R)的图象经过点
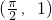 ,求出m,利用两角和的正弦函数化为一个角的一个三角函数的形式,即可得到函数的解析式,然后求出周期和单调增区间.
,求出m,利用两角和的正弦函数化为一个角的一个三角函数的形式,即可得到函数的解析式,然后求出周期和单调增区间.(Ⅱ)利用
 ,求出sinA,l利用面积为
,求出sinA,l利用面积为 ,AB=2,求AC,余弦定理求出BC的长.
,AB=2,求AC,余弦定理求出BC的长.点评:本题是基础题,考查三角函数的正确、单调性、余弦定理的应用,考查计算能力,常考题型.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
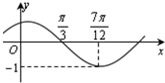 已知函数f(x)=Msin(ωx+φ)(其中
已知函数f(x)=Msin(ωx+φ)(其中