题目内容
已知函数![]() (
(![]() ,实数
,实数![]() ,
,![]() 为常数).
为常数).
(Ⅰ)若![]() (
(![]() ),且函数
),且函数![]() 在
在![]() 上的最小值为0,求
上的最小值为0,求![]() 的值;
的值;
(Ⅱ)若对于任意的实数![]() ,
,![]() ,函数
,函数![]() 在区间
在区间![]() 上总是减函数,对每个给定的n,求
上总是减函数,对每个给定的n,求![]() 的最大值h(n).
的最大值h(n).
解:(1)当![]() 时,
时,![]() .
.
则![]() .
.
令![]() ,得
,得![]() (舍),
(舍),![]() .①当
.①当![]() >1时,
>1时,
|
| 1 |
|
|
|
|
| - | 0 | + | |
|
|
| ↘ |
| ↗ |
∴当![]() 时,
时, ![]() .令
.令![]() ,得
,得![]() .
.
②当![]() 时,
时,![]() ≥0在
≥0在![]() 上恒成立,
上恒成立,
![]() 在
在![]() 上为增函数,当
上为增函数,当![]() 时,
时, ![]() .
.
令![]() ,得
,得![]() (舍).综上所述,所求
(舍).综上所述,所求![]() 为
为![]() .
.
(2) ∵对于任意的实数![]() ,
,![]() ,
,![]() 在区间
在区间![]() 上总是减函数,
上总是减函数,
则对于x∈(1,3),![]() <0, ∴
<0, ∴![]() 在区间[1,3]上恒成立.
在区间[1,3]上恒成立.
设g(x)=![]() , ∵
, ∵![]() ,∴g(x)
,∴g(x)![]() 在区间[1,3]上恒成立.
在区间[1,3]上恒成立.
由g(x)二次项系数为正,得![]() 即
即![]() 亦即
亦即
∵ ![]()
![]() =
=![]() ,
,
∴ 当n<6时,m≤![]() , ,. 当n≥6时,m≤
, ,. 当n≥6时,m≤![]() ,
,
∴ 当n<6时,h(n)= ![]() ,当n≥6时,h(n)=
,当n≥6时,h(n)= ![]() ,即
,即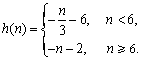

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 (
( ,实数
,实数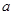 ,
,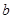 为常数).
为常数).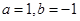 ,求
,求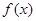 在
在 处的切线方程;
处的切线方程;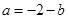 ,讨论函数
,讨论函数 (
( ,实数
,实数 ,
, 为常数).
为常数). ,求函数
,求函数 的极值;
的极值; ,讨论函数
,讨论函数