题目内容
已知P为△ABC所在平面内一点，且满足
=
+
，则△APB的面积与△PAC的面积之比为
．
| AP |
| 1 |
| 5 |
| AC |
| 2 |
| 5 |
| AB |
| 1 |
| 2 |
| 1 |
| 2 |
分析：令
=
，
=
，则
=
+
，可得四边形ADPE是平行四边形，S△PAD=S△PAE，由此可得结论．
| AE |
| 1 |
| 5 |
| AC |
| AD |
| 2 |
| 5 |
| AB |
| AP |
| AE |
| AD |
解答：解：令
=
，
=
，则
=
+
∴四边形ADPE是平行四边形，S△PAD=S△PAE
∵
=
，∴S△PAE=
S△PAC
∵
=
，∴S△PAD=
S△PAB
∴S△PAB：S△PAC=
故答案为：
．
| AE |
| 1 |
| 5 |
| AC |
| AD |
| 2 |
| 5 |
| AB |
| AP |
| AE |
| AD |
∴四边形ADPE是平行四边形，S△PAD=S△PAE
∵
| AE |
| 1 |
| 5 |
| AC |
| 1 |
| 5 |
∵
| AD |
| 2 |
| 5 |
| AB |
| 2 |
| 5 |
∴S△PAB：S△PAC=
| 1 |
| 2 |
故答案为：
| 1 |
| 2 |
点评：本题考查向量知识的运用，考查三角形面积比，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
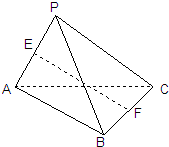已知P为△ABC所在平面外的一点，PC⊥AB，PC=AB=2，E、F分别为PA和BC的中点