题目内容
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为矩形,
为矩形,![]() 平面
平面![]() ,二面角
,二面角![]() 的平面角为
的平面角为![]() ,
,![]() 为
为![]() 中点,
中点,![]() 为
为![]() 中点.
中点.
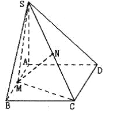
(1)证明:![]() 平面
平面![]() ;
;
(2)证明:平面![]() 平面
平面![]() ;
;
(3)若![]() ,求实数
,求实数![]() 的值,使得直线
的值,使得直线![]() 与平面
与平面![]() 所成角为
所成角为![]() .
.
【答案】(1)详见证明;(2)详见证明;(3)![]() .
.
【解析】
(1)建立空间直角坐标系, 写出坐标,证明![]() 与平面
与平面![]() 的法向量垂直即可;
的法向量垂直即可;
(2)求出平面![]() 与平面
与平面![]() 的法向量,证明平面
的法向量,证明平面![]() 与平面
与平面![]() 的法向量垂直即可;
的法向量垂直即可;
(3)根据直线![]() 与平面
与平面![]() 所成角为
所成角为![]() 建立出关于
建立出关于![]() 的方程,从而求出
的方程,从而求出![]() 的值.
的值.
解:(1)因为![]() 平面
平面![]() ,
,
所以![]() ,
,
又因为底面![]() 为矩形,
为矩形,
所以![]() ,
,
因为![]() ,
,
![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
所以![]() ,
,
因为![]() ,且二面角
,且二面角![]() 的平面角为
的平面角为![]() ,
,
所以![]() ,
,
故![]() ,设
,设![]() ,
,![]() ,
,
因为底面![]() 为矩形,
为矩形,![]() 平面
平面![]() ,
,
故![]() ,
,![]() ,
,
以![]() 为原点,建立如图所示的空间直角坐标系,
为原点,建立如图所示的空间直角坐标系,
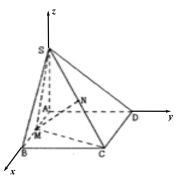
则![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
显然平面![]() 的法向量为
的法向量为![]() ,
,![]()
因为![]() ,
,
所以![]() ,
,
因为![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ;
;
(2)由(1)得![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
故有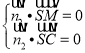 即
即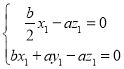
令![]() ,则
,则![]() ,
,
同理,可得平面![]() 的法向量为
的法向量为![]() ,
,
因为![]() ,
,
所以![]() ,
,
所以平面![]() 平面
平面![]() ;
;
(3)因为![]() ,
,
所以![]() ,即
,即![]() ,
,
故![]() ,
,
因为直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
所以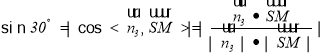 ,
,
即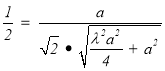 ,
,
化简,解得![]()
因为![]() ,
,
所以![]() .
.

【题目】为了进一步推动全市学习型党组织、学习型社会建设,某市组织开展“学习强国”知识测试,每人测试文化、经济两个项目,每个项目满分均为60分.从全体测试人员中随机抽取了100人,分别统计他们文化、经济两个项目的测试成绩,得到文化项目测试成绩的频数分布表和经济项目测试成绩的频率分布直方图如下:

经济项目测试成绩频率分布直方图
分数区间 | 频数 |
| 2 |
| 3 |
| 5 |
| 15 |
| 40 |
| 35 |
文化项目测试成绩频数分布表
将测试人员的成绩划分为三个等级如下:分数在区间![]() 内为一般,分数在区间
内为一般,分数在区间![]() 内为良好,分数在区间
内为良好,分数在区间![]() 内为优秀.
内为优秀.
(1)在抽取的100人中,经济项目等级为优秀的测试人员中女生有14人,经济项目等级为一般或良好的测试人员中女生有34人.填写下面列联表,并根据列联表判断是否有![]() 以上的把握认为“经济项目等级为优秀”与性别有关?
以上的把握认为“经济项目等级为优秀”与性别有关?
优秀 | 一般或良好 | 合计 | |
男生数 | |||
女生数 | |||
合计 |
(2)用这100人的样本估计总体.
(i)求该市文化项目测试成绩中位数的估计值.
(ii)对该市文化项目、经济项目的学习成绩进行评价.
附:
| 0.150 | 0.050 | 0.010 |
| 2.072 | 3.841 | 6.635 |
![]() .
.
