题目内容
已知: ,cosαcosβ=cosα+cosβ,求:
,cosαcosβ=cosα+cosβ,求: 的值.
的值.
解:cosαcosβ=cosα+cosβ,可得 [cos(α+β)+cos(α-β)]=2
[cos(α+β)+cos(α-β)]=2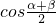

即: [2cos2
[2cos2 -1+2cos2
-1+2cos2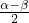 -1]=
-1]=

令 =t 上式化为:t2-
=t 上式化为:t2-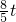 -
- =0 t=
=0 t=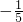 .
.
所以 =
=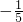 .
.
分析:通过积化和差与和差化积化简cosαcosβ=cosα+cosβ,利用二倍角公式求出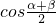 与
与 的关系式,然后求出
的关系式,然后求出 的值.
的值.
点评:本题是基础题,考查积化和差与和差化积公式,二倍角公式的应用,考查计算能力,注意三角函数的值的范围.
 [cos(α+β)+cos(α-β)]=2
[cos(α+β)+cos(α-β)]=2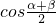

即:
 [2cos2
[2cos2 -1+2cos2
-1+2cos2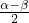 -1]=
-1]=

令
 =t 上式化为:t2-
=t 上式化为:t2-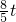 -
- =0 t=
=0 t=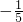 .
.所以
 =
=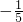 .
.分析:通过积化和差与和差化积化简cosαcosβ=cosα+cosβ,利用二倍角公式求出
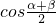 与
与 的关系式,然后求出
的关系式,然后求出 的值.
的值.点评:本题是基础题,考查积化和差与和差化积公式,二倍角公式的应用,考查计算能力,注意三角函数的值的范围.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
 (2011•杭州一模)已知点O为△ABC的外心,角A,B,C的对边分别满足a,b,c,
(2011•杭州一模)已知点O为△ABC的外心,角A,B,C的对边分别满足a,b,c,