题目内容
(06年广东卷)(14分)
设函数![]() 分别在
分别在![]() 、
、![]() 处取得极小值、极大值.
处取得极小值、极大值.![]() 平面上点A、B的坐标分别为
平面上点A、B的坐标分别为![]() 、
、![]() ,该平面上动点P满足
,该平面上动点P满足![]() ,点Q是点P关于直线
,点Q是点P关于直线![]() 的对称点.求:
的对称点.求:
(Ⅰ)点A、B的坐标 ;
(Ⅱ)动点Q的轨迹方程
解析: (Ⅰ)令![]() 解得
解得![]()
当![]() 时,
时,![]() , 当
, 当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]()
所以,函数在![]() 处取得极小值,在
处取得极小值,在![]() 取得极大值,故
取得极大值,故![]() ,
,![]()
所以, 点A、B的坐标为![]() .
.
(Ⅱ) 设![]() ,
,![]() ,
,![]()
![]() ,所以
,所以![]() ,又PQ的中点在
,又PQ的中点在![]() 上,所以
上,所以![]()
消去![]() 得
得![]()

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
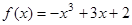 分别在
分别在 、
、 处取得极小值、极大值.
处取得极小值、极大值. 平面上点A、B的坐标分别为
平面上点A、B的坐标分别为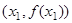 、
、 ,该平面上动点P满足
,该平面上动点P满足 ,点Q是点P关于直线
,点Q是点P关于直线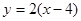 的对称点
的对称点