题目内容
在△ABC中,∠A=60°,点M为边AC的中点,BM=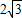 ,则AB+AC的最大值为 .
,则AB+AC的最大值为 .
【答案】分析:依题意,利用正弦定理可求得△ABM的外接圆直径,从而可用角表示出AB,AC,利用三角函数间的关系式即可求得AB+AC的最大值.
解答:解:∵在△ABC中,∠A=60°,点M为边AC的中点,BM=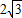 ,
,
∴在△ABM中,设∠AMB=θ,则∠ABM=120°-θ,0<θ<120°,
由正弦定理得: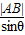 =
=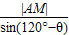 =
=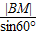 =
=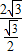 =4,
=4,
∴|AB|=4sinθ,|AM|=4sin(120°-θ),又点M为边AC的中点,
∴|AC|=2|AM|=8sin(120°-θ),
∴|AB|+|AC|=4sinθ+8sin(120°-θ)
=4sinθ+8×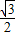 cosθ-8×(-
cosθ-8×(- )sinθ
)sinθ
=8sinθ+4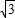 cosθ
cosθ
=4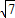 sin(θ+φ),(其中tanφ=
sin(θ+φ),(其中tanφ=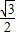 ).
).
∴当sin(θ+φ)=1时,|AB|+|AC|取得最大值.
∴|AB|+|AC|的最大值为4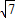 .
.
故答案为:4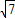 .
.
点评:本题考查正弦定理的应用,考查三角函数间的关系式及辅助角公式的应用,能用三角关系式表示出AB+AC是关键,也是难点,属于中档题.
解答:解:∵在△ABC中,∠A=60°,点M为边AC的中点,BM=
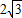 ,
,∴在△ABM中,设∠AMB=θ,则∠ABM=120°-θ,0<θ<120°,
由正弦定理得:
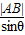 =
=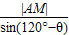 =
=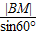 =
=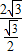 =4,
=4,∴|AB|=4sinθ,|AM|=4sin(120°-θ),又点M为边AC的中点,
∴|AC|=2|AM|=8sin(120°-θ),
∴|AB|+|AC|=4sinθ+8sin(120°-θ)
=4sinθ+8×
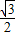 cosθ-8×(-
cosθ-8×(- )sinθ
)sinθ=8sinθ+4
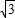 cosθ
cosθ=4
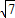 sin(θ+φ),(其中tanφ=
sin(θ+φ),(其中tanφ=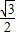 ).
).∴当sin(θ+φ)=1时,|AB|+|AC|取得最大值.
∴|AB|+|AC|的最大值为4
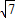 .
.故答案为:4
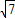 .
.点评:本题考查正弦定理的应用,考查三角函数间的关系式及辅助角公式的应用,能用三角关系式表示出AB+AC是关键,也是难点,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目