题目内容
若直角坐标系中有两点P，Q满足条件：（1）P，Q分别在函数y=f（x）、y=g（x）的图象上，（2）P，Q关于点（1，0）对称，则称P，Q是一个“和谐点对”．函数y=
的图象与函数y=2sinπx（-2≤x≤4）的图象中“和谐点对”的个数是（ ）
| 1 | 1-x |
分析：作出两函数图象，借助图象的对称性及“和谐点对”的定义可得答案．
解答：
解：作出函数y=
与y=2sinπx（-2≤x≤4）的图象，
由图象可知两函数图象有8个交点，
又y=
与y=2sinπx（-2≤x≤4）图象都关于（1，0）点对称，
∴交点也关于（1，0）对称，
由图象及“和谐点对”的定义可知“和谐点对”的个数是4个，
故选A．
解：作出函数y=| 1 |
| 1-x |
由图象可知两函数图象有8个交点，
又y=
| 1 |
| 1-x |
∴交点也关于（1，0）对称，
由图象及“和谐点对”的定义可知“和谐点对”的个数是4个，
故选A．
点评：本题考查函数的图象及其应用，考查学生分析解决新问题的能力．
练习册系列答案
春雨教育同步作文系列答案
相关题目
满足条件：（1）
、
的图象上，（2）
的图象与函数
的图象中“和谐点对”的个数是（ ）
中有两定点
，
，若动点M满足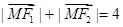
，设动点M的轨迹为C。
交曲线C于A、B两点，交直线
于点D，若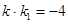
，证明：D为AB的中点。