题目内容
设a,b∈R,a+2i=
,则
等于( )
| -1+bi |
| 3-i |
| lim |
| n→∞ |
| an-bn |
| an+bn |
| A、2 | B、-1或1 |
| C、-1 | D、不存在 |
分析:利用复数的除法运算化简已知等式右边,然后利用复数相等的条件求解a,b的值,代入要求解极限的代数式后求解极限值.
解答:解:由a+2i=
,得
a+2i=
=
=
+
i,
又a,b∈R,
∴
,解得:
.
∴
=
=
=-1.
故选:C.
| -1+bi |
| 3-i |
a+2i=
| (-1+bi)(3+i) |
| (3-i)(3+i) |
| (-3-b)+(3b-1)i |
| 10 |
| -3-b |
| 10 |
| 3b-1 |
| 10 |
又a,b∈R,
∴
|
|
∴
| lim |
| n→∞ |
| an-bn |
| an+bn |
| lim |
| n→∞ |
| (-1)n-7n |
| (-1)n+7n |
| lim |
| n→∞ |
| ||
|
故选:C.
点评:本题考查了复数代数形式的乘除运算,考查了复数相等的条件,训练了数列极限的求法,是基础题.

练习册系列答案
相关题目
设a,b∈R且a≠2若定义在区间(-b,b)上的函数f(x)=lg
是奇函数.则a+b的取值范围是( )
| 1+ax |
| 1+2x |
A、(0,
| ||
B、(-2,-
| ||
C、(2,
| ||
D、(-2,-
|
 在区间(-b,b)上是奇函数.
在区间(-b,b)上是奇函数.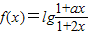 在区间(-b,b)上是奇函数.
在区间(-b,b)上是奇函数.