题目内容
设a,b∈R,a≠2,若定义在(-b,b)内的函数f(x)=lg
是奇函数,则a+b的取值范围是( )
| 1+ax |
| 1+2x |
分析:已知定义在(-b,b)内的函数f(x)=lg
是奇函数,可得f(-x)=-f(x),可求出a的值,从而求解.
| 1+ax |
| 1+2x |
解答:解:∵定义在(-b,b)内的函数f(x)=lg
是奇函数,
∴f(-x)=lg
=-f(x)=-lg
=lg
,
∴a=-2,
∴f(x)=lg
,
∴
>0,
∴-
<x<
,∵f(x)的定义域为(-b,b),
∴b≤
,∴a+b=b-2≤
-2=-
,
∵b-2>-2,
∴-2<a+b≤-
,
故选B.
| 1+ax |
| 1+2x |
∴f(-x)=lg
| 1-ax |
| 1-2x |
| 1+ax |
| 1+2x |
| 1+2x |
| 1+ax |
∴a=-2,
∴f(x)=lg
| 1-2x |
| 1+2x |
∴
| 1-2x |
| 1+2x |
∴-
| 1 |
| 2 |
| 1 |
| 2 |
∴b≤
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∵b-2>-2,
∴-2<a+b≤-
| 3 |
| 2 |
故选B.
点评:此题主要考查函数奇偶性的性质,要知道偶函数的性质f(-x)=f(x),奇函数的性质f(-x)=-f(x),此题是一道好题.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
设a,b∈R且a≠2若定义在区间(-b,b)上的函数f(x)=lg
是奇函数.则a+b的取值范围是( )
| 1+ax |
| 1+2x |
A、(0,
| ||
B、(-2,-
| ||
C、(2,
| ||
D、(-2,-
|
 在区间(-b,b)上是奇函数.
在区间(-b,b)上是奇函数.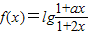 在区间(-b,b)上是奇函数.
在区间(-b,b)上是奇函数.