题目内容
已知y=(1+cos2x)2，求
.
思路分析：注意2x与x系数不一样，也有一个复合的过程，容易忽视，造成错误.?
解：设y=u2,u=(1+cos2x),?
则yx′=yu′·ux′?
=2u(1+cos2x)′?
=2u·(-sin2x)·2?
=-4sin2x(1+cos2x),?
所以y′=-4sin2x(1+cos2x).?
练习册系列答案
相关题目
已知f(x)=cos(ωx+
)，(ω＞0)的图象与y=1的图象的两相邻交点间的距离为π，要得到y=f（x）的图象，只须把y=sinωx的图象（ ）
| π |
| 3 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
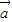=（cosωx-sinωx，sinωx），
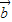=（-cosωx-sinωx，2
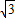cosωx），设函数f（x）=
•
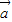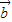+λ（x∈R）的图象关于直线x=π对称，其中ω，λ为常数，且ω∈（
，1）
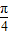，0）求函数f（x）在区间[0，
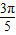]上的取值范围．
=（cosωx-sinωx，sinωx），
=（-cosωx-sinωx，2
cosωx），设函数f（x）=
•
+λ（x∈R）的图象关于直线x=π对称，其中ω，λ为常数，且ω∈（
，1）
，0）求函数f（x）在区间[0，
]上的取值范围．