题目内容
指数函数①f(x)=mx;②g(x)=nx满足不等式1>n>m>0,则它们的图象是( )
解析:此题应首先根据底数的范围判断图象的升降性,再根据两个底数的大小比较判断对应的曲线.
由0<m<n<1可知①②应为两条递减的曲线,故只可能是C或D,进而再判断①②与n和m的对应关系,此时判断的方法很多,不妨选特殊点法,令x=1,①②对应的函数值分别为m和n,由m<n可知应选C.
答案:C

练习册系列答案
相关题目
若指数函数f(x)=ax(a>0且a≠1)的部分对应值如下表:
x | -2 | 0 |
f(x) | 0.592 | 1 |
则不等式f-1(|x|)<0的解集为
A.{x|-1<x<1} B.{x|x<-1或x>1}
C.{x|0<x<1} D.{x|-1<x<0或0<x<1}
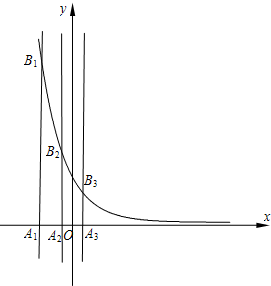 (2006•蚌埠二模)已知等差数列{an}的首项为p,公差为d(d>0).对于不同的自然数n,直线x=an与x轴和指数函数
(2006•蚌埠二模)已知等差数列{an}的首项为p,公差为d(d>0).对于不同的自然数n,直线x=an与x轴和指数函数 (2005•静安区一模)已知等差数列{an}的首项为p,公差为d(d>0).对于不同的自然数n,直线x=an与x轴和指数函数
(2005•静安区一模)已知等差数列{an}的首项为p,公差为d(d>0).对于不同的自然数n,直线x=an与x轴和指数函数