题目内容

过双曲线C：x2-
y2
3
=1的右焦点F作直线L与双曲线C交于P、Q两点，
OM
=
OP
+
OQ
，则点M的轨迹方程为
（x-1）2-
y2
12
=1
（x-1）2-
y2
12
=1
．
分析：设出直线的方程与双曲线方程联立求得x和y，消去k求得x和y的关系，进而求得M的轨迹方程．
解答：解：令直线方程：ky=x-2  
联立方程组解得：（3k2-1）y2+12ky+9=0
令p（x1，y1）  q（x2，y2）  m（x，y）
由题意：x=x1+x2    y=y1+y2
所以 x=-
2
3k2-1
  y=--
12k
3k2-1
  
消去k得：（x-1）2-
y2
12
=1
故点M的轨迹方程：（x-1）2-
y2
12
=1
故答案为：（x-1）2-
y2
12
=1
点评：本题主要考查了双曲线的简单性质以及直线与双曲线的关系．考查了基础知识的综合运用．
练习册系列答案
相关题目
给出下列命题：
①已知椭圆
x2
16
+
y2
8
=1的两个焦点为F1，F2，则这个椭圆上存在六个不同的点M，使得△F1MF2为直角三角形；
②已知直线l过抛物线y=2x2的焦点，且与这条抛物线交于A，B两点，则|AB|的最小值为2；
③若过双曲线C：
x2
a2
-
y2
b2
=1(a＞0，b＞0)的一个焦点作它的一条渐近线的垂线，垂足为M，O为坐标原点，则|OM|=a；
④已知⊙C1：x2+y2+2x=0，⊙C2：x2+y2+2y-1=0，则这两个圆恰有2条公切线．
其中正确命题的序号是
 
．（把你认为正确命题的序号都填上）
双曲线C：x2-y2=1的渐近线方程为
x±y=0
x±y=0
；若双曲线C的右顶点为A，过A的直线l与双曲线C的两条渐近线交于P，Q两点，且
PA
=2
AQ
，则直线l的斜率为
±3
±3
．
给出下列命题：
①已知椭圆
x2
16
+
y2
8
=1的两个焦点为F1，F2，则这个椭圆上存在六个不同的点M，使得△F1MF2为直角三角形；
②已知直线l过抛物线y=2x2的焦点，且与这条抛物线交于A，B两点，则|AB|的最小值为2；
③若过双曲线C：
x2
a2
-
y2
b2
=1(a＞0，b＞0)的一个焦点作它的一条渐近线的垂线，垂足为M，O为坐标原点，则|OM|=a；
④已知⊙C1：x2+y2+2x=0，⊙C2：x2+y2+2y-1=0，则这两个圆恰有2条公切线．
其中正确命题的序号是______．（把你认为正确命题的序号都填上）
给出下列命题：
①已知椭圆的两个焦点为F1，F2，则这个椭圆上存在六个不同的点M，使得△F1MF2为直角三角形；
②已知直线l过抛物线y=2x2的焦点，且与这条抛物线交于A，B两点，则|AB|的最小值为2；
③若过双曲线C：的一个焦点作它的一条渐近线的垂线，垂足为M，O为坐标原点，则|OM|=a；
④已知⊙C1：x2+y2+2x=0，⊙C2：x2+y2+2y-1=0，则这两个圆恰有2条公切线．
其中正确命题的序号是    ．（把你认为正确命题的序号都填上）
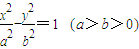已知双曲线C：和圆O：x2+y2=b2（其中原点O为圆心），过双曲线C上一点P（x，y）引圆O的两条切线，切点分别为A、B．
（1）若双曲线C上存在点P，使得∠APB=90°，求双曲线离心率e的取值范围；
（2）求直线AB的方程；
（3）求三角形OAB面积的最大值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网