题目内容
设a∈R,f(x)=x3-x2-x+a,曲线y=f(x)与x轴有且只有一个公共点,实数a的取值范围是 .
【答案】分析:要使函数f(x)=x3-x2-x+a的图象与直线x轴只有一个公共点,只需利用函数的最大值或最小值与0进行比较,由于实数a的值不确定,故要分类讨论.
解答:解:求一阶导数可得f'(x)=3x2-2x-1,
两个极值点分别在x=1、x=- ,
,
代入函数,得f(1)=a-1,f(- )=a+
)=a+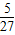 ,
,
当a-1>0时,f(1)>0,得出a>1,
当a+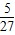 <0时,f(-
<0时,f(- )<0,得出a<-
)<0,得出a<-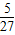 ,
,
则曲线y=f(x)与x轴有且只有一个公共点,实数a的取值范围为: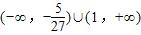 ,
,
故答案为: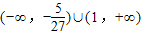 .
.
点评:本题主要考查函数的单调性、极值以及函数导数的应用,考查运用数学知识分析问题解决问题的能力.
解答:解:求一阶导数可得f'(x)=3x2-2x-1,
两个极值点分别在x=1、x=-
 ,
,代入函数,得f(1)=a-1,f(-
 )=a+
)=a+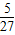 ,
,当a-1>0时,f(1)>0,得出a>1,
当a+
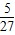 <0时,f(-
<0时,f(- )<0,得出a<-
)<0,得出a<-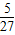 ,
,则曲线y=f(x)与x轴有且只有一个公共点,实数a的取值范围为:
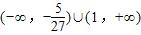 ,
,故答案为:
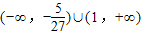 .
.点评:本题主要考查函数的单调性、极值以及函数导数的应用,考查运用数学知识分析问题解决问题的能力.

练习册系列答案
相关题目