题目内容
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,焦距为
,焦距为![]() .斜率为
.斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 有两个不同的交点
有两个不同的交点![]() ,
,![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 的另一个交点为
的另一个交点为![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 的另一个交点为
的另一个交点为![]() .若
.若![]() ,
,![]() 和点
和点![]() 共线,求
共线,求![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)根据离心率和焦距求得![]() ,由此求得
,由此求得![]() ,进而求得椭圆
,进而求得椭圆![]() 的标准方程.
的标准方程.
(2)设出直线![]() 的方程,联立直线
的方程,联立直线![]() 的方程和椭圆方程,写出根与系数关系,进而求得
的方程和椭圆方程,写出根与系数关系,进而求得![]() 点的坐标,同理求得
点的坐标,同理求得![]() 点坐标.求得
点坐标.求得![]() 、
、![]() ,结合
,结合![]() 三点共线列方程,化简求得
三点共线列方程,化简求得![]() 的值.
的值.
(1)由题意得![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
所以椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)设![]() ,
,![]() ,
,![]() ,
,![]() ,
,
则![]() ①,
①,![]() ②,
②,
又![]() ,所以可设
,所以可设![]() ,
,
直线![]() 的方程为
的方程为![]() ,
,
由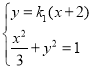 消去
消去![]() 可得:
可得:
![]() ,
,
则![]() ,即
,即![]() ,
,
又![]() ,代入①式可得
,代入①式可得![]() ,
,
所以![]() ,所以
,所以![]() ,
,
同理可得![]() .
.
故![]() ,
,![]() ,
,
因为![]() 三点共线,
三点共线,
所以![]() ,
,
将点![]() 的坐标代入化简可得
的坐标代入化简可得![]() ,
,
即![]() .
.

练习册系列答案
相关题目
【题目】某商场为了了解顾客的购物信息,随机在商场收集了![]() 位顾客购物的相关数据如下表:
位顾客购物的相关数据如下表:
一次购物款(单位:元) |
|
|
|
|
|
顾客人数 |
|
|
|
|
|
统计结果显示![]() 位顾客中购物款不低于
位顾客中购物款不低于![]() 元的顾客占
元的顾客占![]() ,该商场每日大约有
,该商场每日大约有![]() 名顾客,为了增加商场销售额度,对一次购物不低于
名顾客,为了增加商场销售额度,对一次购物不低于![]() 元的顾客发放纪念品.
元的顾客发放纪念品.
(Ⅰ)试确定![]() ,
, ![]() 的值,并估计每日应准备纪念品的数量;
的值,并估计每日应准备纪念品的数量;
(Ⅱ)为了迎接春节,商场进行让利活动,一次购物款![]() 元及以上的一次返利
元及以上的一次返利![]() 元;一次购物不超过
元;一次购物不超过![]() 元的按购物款的百分比返利,具体见下表:
元的按购物款的百分比返利,具体见下表:
一次购物款(单位:元) |
|
|
|
|
返利百分比 |
|
|
|
|
请问该商场日均大约让利多少元?