题目内容
20.f(x)是定义在(0,+∞)上的增函数,且f($\frac{x}{y}$)=f(x)-f(y).若f(2)=1,解关于x的不等式f(x+3)-f($\frac{1}{x}$)<2.分析 若f(2)=1,结合抽象函数将不等式化为f(x+3)-f($\frac{1}{x}$)<f(2)+f(2),再进行转化,结合函数的单调性解不等式即可.
解答 解:∵f(2)=1,∴2=1+1=f(2)+f(2),
对于不等式f(x+3)-f($\frac{1}{x}$)<2,有$\left\{\begin{array}{l}{x+3>0}\\{\frac{1}{x}>0}\end{array}\right.$,
解可得x>0,
∴不等式f(x+3)-f($\frac{1}{x}$)<2,
等价为不等式f(x+3)-f($\frac{1}{x}$)<f(2)+f(2),
∴f(x2+3x)-f(2)<f(2),
即f($\frac{{x}^{2}+3x}{2}$)<f(2),
∵f(x)是(0,+∞)上的增函数,
∴0<$\frac{{x}^{2}+3x}{2}$<2,解得-4<x<-3或0<x<1,
又由x>0,
即不等式的解集为(0,1).
点评 本题主要考查抽象函数的应用,根据函数单调性将不等式进行转化是解决本题的关键.

练习册系列答案
相关题目
5.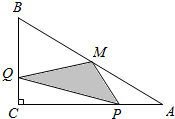 如图,△ABC中,∠C=90°,M是AB的中点,动点P从点A出发,沿AC方向匀速运动到终点C,动点Q从点C出发,沿CB方向匀速运动到终点B.已知P,Q两点同时出发,并同时到达终点,连接MP,MQ,PQ.在整个运动过程中,△MPQ的面积大小变化情况是( )
如图,△ABC中,∠C=90°,M是AB的中点,动点P从点A出发,沿AC方向匀速运动到终点C,动点Q从点C出发,沿CB方向匀速运动到终点B.已知P,Q两点同时出发,并同时到达终点,连接MP,MQ,PQ.在整个运动过程中,△MPQ的面积大小变化情况是( )
 如图,△ABC中,∠C=90°,M是AB的中点,动点P从点A出发,沿AC方向匀速运动到终点C,动点Q从点C出发,沿CB方向匀速运动到终点B.已知P,Q两点同时出发,并同时到达终点,连接MP,MQ,PQ.在整个运动过程中,△MPQ的面积大小变化情况是( )
如图,△ABC中,∠C=90°,M是AB的中点,动点P从点A出发,沿AC方向匀速运动到终点C,动点Q从点C出发,沿CB方向匀速运动到终点B.已知P,Q两点同时出发,并同时到达终点,连接MP,MQ,PQ.在整个运动过程中,△MPQ的面积大小变化情况是( )| A. | 一直增大 | B. | 一直减小 | C. | 先减小后增大 | D. | 先增大后减小 |
12.已知集合A={x|x2-x-2≤0},B={y|y=2x,x∈A},则A∩B=( )
| A. | [-1,2] | B. | [-1,4] | C. | [$\frac{1}{2}$,4] | D. | [$\frac{1}{2}$,2] |
10.已知点G是△ABC的重心,且AG⊥BG,若λ=$\frac{si{n}^{2}C}{cosCsinAsinB}$,则实数λ的值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | 3 | D. | 2 |
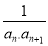 }的前100项和为
}的前100项和为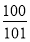 B.
B.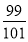 C.
C.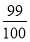 D.
D.