Question

已知圆x²+y²-9x=0与顶点在原点O、焦点在x轴上的抛物线交于异于原点的A、B两点,△AOB的垂心恰为抛物线的焦点,求抛物线C的方程.

Answer 1

解:由圆的方程x²+y²-9x=0,可知该圆的圆心坐标为(3,0),半径r=3.

∵抛物线与该圆相交,且焦点在x轴上,

∴抛物线的方程可以设为y²=2px(p＞0).

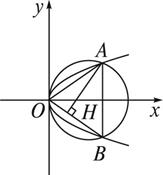
如图所示,由点A向OB引垂线,与x轴交于点H,根据抛物线与圆的对称性可知,H即为△AOB的垂心,亦即为F,设A(x₀,y₀),则B(x₀,-y₀).

∵点A、B是抛物线和圆的公共点,则2px₀=y₀²,

∴A(x₀,),B(x₀,-)且x₀²+2px₀-9x₀=0.

∵x₀≠0,∴x₀=9-2p.①

又∵k_OB·k_AH=-1,即·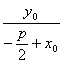=-1,

∴y₀²=x₀(-+x₂)=2px₀.

∴x₀=.②

由①②可得p=2,故所求抛物线的方程为y²=4x.