题目内容
已知向量a=（1，0），b=（0，1），c=a+λb（λ∈R），向量d如图所示．则
- A.存在λ＞0，使得向量c与向量d垂直
- B.存在λ＞0，使得向量c与向量d夹角为60°
- C.存在λ＜0，使得向量c与向量d夹角为30°
- D.存在λ＞0，使得向量c与向量d共线
D
分析：利用向量垂直的充要条件：数量积为0，判断出A错；利用向量的数量积的坐标公式及模，夹角公式判断出B，C错；利用向量共线的充要条件判断出D对．
解答：由图知，
，则
若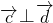
则4+3λ=0得
，故A错
若夹角为60°则有
即11λ2+96λ+39=0，有两个负根；故B错；
若夹角为30°，则有
即39λ2-96λ+9=0有两个正根，故C错；
若两个向量共线则有4λ=3解得
，故D对．
故选D
点评：本题考查向量垂直的充要条件：数量积为0即对应的坐标相乘等于0；向量共线的充要条件：坐标交叉相乘相等．
分析：利用向量垂直的充要条件：数量积为0，判断出A错；利用向量的数量积的坐标公式及模，夹角公式判断出B，C错；利用向量共线的充要条件判断出D对．
解答：由图知，
，则若
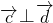则4+3λ=0得，故A错若夹角为60°则有
即11λ2+96λ+39=0，有两个负根；故B错；若夹角为30°，则有
即39λ2-96λ+9=0有两个正根，故C错；若两个向量共线则有4λ=3解得
，故D对．故选D
点评：本题考查向量垂直的充要条件：数量积为0即对应的坐标相乘等于0；向量共线的充要条件：坐标交叉相乘相等．
练习册系列答案
数学奥赛暑假天天练南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
已知向量
=（1，0）与向量
=（-1，
），则向量
与
的夹角为（ ）
| a |
| b |
| 3 |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|