题目内容
三棱锥P-ABC的各顶点都在一半径为R的球面上，球心O在AB上，且有PA=PB=PC，底面△ABC中∠ABC=60°，则球与三棱锥的体积之比是______．
三棱锥P-ABC的各顶点都在一半径为R的球面上，
球心O在AB上，且有PA=PB=PC，底面△ABC中∠ABC=60°，
所以AB为球的直径，PO为三棱锥的高，
三棱锥的底面面积为：
•R•2R•sin60°=
R2，
三棱锥的体积为：
×
R3=
；
球的体积：
R3
球与三棱锥的体积之比是：
=
故答案为：
球心O在AB上，且有PA=PB=PC，底面△ABC中∠ABC=60°，
所以AB为球的直径，PO为三棱锥的高，
三棱锥的底面面积为：
| 1 |
| 2 |
| ||
| 2 |
三棱锥的体积为：
| 1 |
| 3 |
| ||
| 2 |
| ||
| 6 |
球的体积：
| 4π |
| 3 |
球与三棱锥的体积之比是：
| ||||
|
8
| ||
| 3 |
故答案为：
8
| ||
| 3 |
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
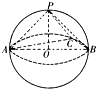如图所示，已知三棱锥P-ABC的各顶点均在一个半径为R的球面上，球心0在AB上，P0⊥平面ABC，