题目内容

已知点A（4，-2），F为抛物线y2=8x的焦点，点M在抛物线上移动，当|MA|+|MF|取最小值时，点M的坐标为（    ）

A.（0，0）                                     B.（1，-2）

C.（2，-2）                                    D.（，-2）

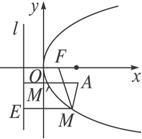
解析：如图所示，过M作准线l的垂线，垂足为E，由抛物线定义知|MF|=|ME|，当M在抛物线上移动时，|ME|+|MA|的值在变化，显然当M移到M′时，A、M、E共线，|ME|+|MA|最小，此时AM′∥Ox轴，把y=-2代入y2=8x，得x=.

所以M′（，-2）.故选D.

答案：D

练习册系列答案
相关题目
给出以下命题：
①过点P（2，3），且与圆（x-1）2+（y-1）2=1相切的直线方程为3x-4y+6=0；
②双曲线
y2
49
-
x2
25
=-1的渐近线方程为y=±
7
5
x；
③不等式
1-2x
(x-1)(x+3)
≤0的解集为{x|x＜-3或
1
2
≤x＜1}；
④已知点A（4，-2），抛物线y2=8x的焦点为F，点M在抛物线上移动，则|MA|+|MF|的最小值为6．
其中正确命题的序号是
②④
②④
．
已知点A（1，-2，11），B（4，2，3），C（6，-1，4），则△ABC的形状是（　　）
A、等边三角形B、直角三角形C、等腰三角形D、等腰直角三角形
已知点A（0，-2），B（0，4），动点P（x，y）满足
PA
•
PB
=y2-8；
（1）求动点P的轨迹方程；
（2）设（1）中所求轨迹方程与直线y=x+2交于C、D两点；求证OC⊥OD（O为坐标原点）．
已知点A（4，3）和圆C：（x-2）2+y2=4
（1）求圆C关于点A对称的圆C1的标准方程；
（2）求过点A并且与圆C相切的直线方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网