题目内容

设点(p,q)在|p|≤3,|q|≤3中按均匀分布出现,试求方程x2+2px-q2+1=0的两根都是实数的概率.

解：根据一元二次方程有实数根的充要条件找出p,q的约束条件,从而确定区域的几何度量.由已知,点(p,q)组成了边长为6的正方形,所以D=62=36.由方程x2+2px-q2+1=0两根都是实数得:Δ=(2p)2-4(-q2+1)≥0,即p2+q2≥1.所以当点(p,q)落在“正方形内且圆外”的阴影区域时，方程的两根都是正数.

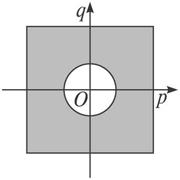
由图可知，阴影部分面积d=S正方形-S圆=36-π.所以原方程两根都是实数的概率为P=≈0.91.

温馨提示

    这里把一个方程根的问题转化为平面区域上图形的面积问题,从而使问题得到了解决,这里的转化起到了“化抽象为具体”的作用.

练习册系列答案
相关题目
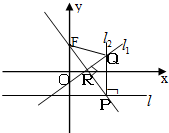（2012•威海二模）如图，在平面直角坐标系xoy中，设点F（0，p）（p＞0），直线l：y=-p，点p在直线l上移动，R是线段PF与x轴的交点，过R、P分别作直线l1、l2，使l1⊥PF，l2⊥l l1∩l2=Q．
（Ⅰ）求动点Q的轨迹C的方程；
（Ⅱ）在直线l上任取一点M做曲线C的两条切线，设切点为A、B，求证：直线AB恒过一定点；
（Ⅲ）对（Ⅱ）求证：当直线MA，MF，MB的斜率存在时，直线MA，MF，MB的斜率的倒数成等差数列．
（2013•徐汇区一模）已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的一个焦点为F（1，0），点（-1，
2
2
）在椭圆C上，点T满足
OT
=
a2
a2-b2
•
OF
（其中O为坐标原点），过点F作一直线交椭圆于P、Q两点．
（1）求椭圆C的方程；
（2）求△PQT面积的最大值；
（3）设点P′为点P关于x轴的对称点，判断
PQ
与
QT
的位置关系，并说明理由．
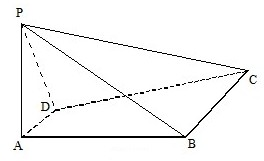精英家教网如图，四棱锥P-ABCD中，PA⊥平面ABCD，四边形ABCD是直角梯形，其中DA⊥AB，AD∥BC．PA=2AD=BC=2AB=2
2
．
（1）求异面直线PC与AD所成角的大小；
（2）若平面ABCD内有一经过点C的曲线E，该曲线上的任一动点Q都满足PQ与AD所成角的大小恰等PC与AD所成角．试判断曲线E的形状并说明理由；
（3）在平面ABCD内，设点Q是（2）题中的曲线E在直角梯形ABCD内部（包括边界）的一段曲线CG上的动点，其中G为曲线E和DC的交点．以B为圆心，BQ为半径的圆分别与梯形的边AB、BC交于M、N两点．当Q点在曲线段GC上运动时，试提出一个研究有关四面P-BMN的问题（如体积、线面、面面关系等）并尝试解决．
（说明：本小题将根据你提出的问题的质量和解决难度分层评分；本小题的计算结果可以使用近似值，保留3位小数）

设点P点在圆C：上移动，点Q（2，0）内分所成比

为2∶1，将逆时针方向转90°到QH，

   （1）求R点轨迹方程

   （2）求|RH|的最大值

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网