题目内容
已知圆 的方程为
的方程为 ,且
,且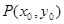 在圆
在圆 外,圆
外,圆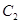 的方程为
的方程为
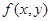 =
= ,则
,则 与圆
与圆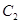 一定
一定

 A.相离
B.相切 C.同心圆 D.相交
A.相离
B.相切 C.同心圆 D.相交
【答案】
C
【解析】
试题分析:因为C1为圆,则f(x,y)=0必具有f(x,y)=x2+y2+Dx+Ey+F=0 ,
其圆心为( ,
, ) ;
) ;
而C2的方程为 f(x,y)-f(x0,y0)=0 ,即 x2+y2+Dx+Ey+(F-x02-y02-Dx0-Ey0-F)=0 ,
F-x02-y02-Dx0-Ey0-F是常数项 ,因此上述方程中,圆心亦为( ,
, ),所以C1与圆C2是同心圆,故选C。
),所以C1与圆C2是同心圆,故选C。
考点:本题主要考查圆与圆的位置关系
点评:由题意设出圆C1的方程为f(x,y)=0,求出圆心,半径,表示出圆C2的方程为f(x,y)=f(x0,y0),推出二者是同心圆即可。

练习册系列答案
相关题目