题目内容
设函数f(x)=x(x-a)2,(I)证明:a<3是函数f(x)在区间(1,2)上递减的必要而不充分的条件;
(II)若x∈[0,|a|+1]时,f(x)<2a2恒成立,且f(0)=0,求实数a的取值范围.
【答案】分析:(I)先求函数f(x)在区间(1,2)上递减的充要条件,
f(x)在区间(1,2)上递减?f'(x)=3x2-4ax+a2≤0在区间(1,2)上恒成立,处理二次不等式恒成立问题可用实根分布求解.
(II)x∈[0,|a|+1]时,f(x)<2a2恒成立?f(x)max<2a2,x∈[0,|a|+1],问题转化为求函数的最值问题.
解答:解:(I)∵f(x)在区间(1,2)上递减,
∴其导函数f'(x)=3x2-4ax+a2≤0在区间(1,2)上恒成立.
∴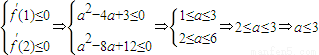
故a≤3是函数f(x)在区间(1,2)上递减的必要而不充分的条件
解法二:f'(x)=3x2-4ax+a2=(3x-a)(x-a)≤0在区间(1,2)上恒成立,
∴a只能大于0,∴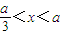 ,∴
,∴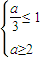 ∴2≤a≤3⇒a≤3
∴2≤a≤3⇒a≤3
故a≤3是函数f(x)在区间(1,2)上递减的必要而不充分的条件
(II)∵f(x)=x(x-a)2
当a>0时,函数y=f(x)在(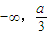 )上递增,
)上递增,
在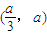 上递减,在
上递减,在 上递增,
上递增,
故有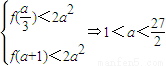
当a<0时,函数y=f(x)在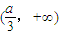 上递增,
上递增,
∴只要f(1-a)<2a2⇒4a3-6a2+5a-1>0
令g(a)=4a3-6a2+5a-1,
则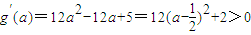
所以g(a)在(-∞,0)上递增,
又g(0)=-1<0∴f(1-a)<2a2不能恒成立
故所求的a的取值范围为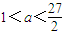
点评:本题考查已知函数的单调区间求参数范围问题和不等式恒成立问题,体现分类讨论和化归思想.
f(x)在区间(1,2)上递减?f'(x)=3x2-4ax+a2≤0在区间(1,2)上恒成立,处理二次不等式恒成立问题可用实根分布求解.
(II)x∈[0,|a|+1]时,f(x)<2a2恒成立?f(x)max<2a2,x∈[0,|a|+1],问题转化为求函数的最值问题.
解答:解:(I)∵f(x)在区间(1,2)上递减,
∴其导函数f'(x)=3x2-4ax+a2≤0在区间(1,2)上恒成立.
∴
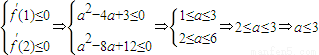
故a≤3是函数f(x)在区间(1,2)上递减的必要而不充分的条件
解法二:f'(x)=3x2-4ax+a2=(3x-a)(x-a)≤0在区间(1,2)上恒成立,
∴a只能大于0,∴
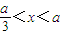 ,∴
,∴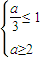 ∴2≤a≤3⇒a≤3
∴2≤a≤3⇒a≤3故a≤3是函数f(x)在区间(1,2)上递减的必要而不充分的条件
(II)∵f(x)=x(x-a)2

当a>0时,函数y=f(x)在(
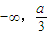 )上递增,
)上递增,在
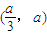 上递减,在
上递减,在 上递增,
上递增,故有
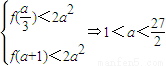
当a<0时,函数y=f(x)在
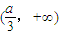 上递增,
上递增,∴只要f(1-a)<2a2⇒4a3-6a2+5a-1>0
令g(a)=4a3-6a2+5a-1,
则
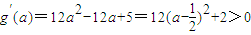
所以g(a)在(-∞,0)上递增,
又g(0)=-1<0∴f(1-a)<2a2不能恒成立
故所求的a的取值范围为
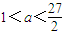
点评:本题考查已知函数的单调区间求参数范围问题和不等式恒成立问题,体现分类讨论和化归思想.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
设函数f(x)的定义域为A,若存在非零实数t,使得对于任意x∈C(C⊆A),有x+t∈A,且f(x+t)≤f(x),则称f(x)为C上的t低调函数.如果定义域为[0,+∞)的函数f(x)=-|x-m2|+m2,且 f(x)为[0,+∞)上的10低调函数,那么实数m的取值范围是( )
| A、[-5,5] | ||||||||
B、[-
| ||||||||
C、[-
| ||||||||
D、[-
|