题目内容
已知实数a为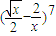 的展开式中x2的系数,则
的展开式中x2的系数,则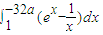 = .
= .
【答案】分析:先求出二项展开式得通项,令x得指数为2求出r,进而求出a,再代入 利用定积分知识求解即可.
利用定积分知识求解即可.
解答:解:因为 的展开式得通项为:Tr+1=
的展开式得通项为:Tr+1=
 •
• =(-1)r
=(-1)r •
• •2r•
•2r• •x-r;
•x-r;
令 =2⇒r=1.
=2⇒r=1.
∴展开式中x2的系数为:(-1)1× •
• •21=-
•21=- .
.
∴a=- .
.
∴ =
= (ex-
(ex- )dx═(ex-lnx)|
)dx═(ex-lnx)| =(e7-ln7)-(e1-ln1)=e7-ln7-e.
=(e7-ln7)-(e1-ln1)=e7-ln7-e.
故答案为:e7-ln7-e.
点评:本题主要考查二项展开式的应用问题.解决问题的关键在于熟悉求二项展开式的通项,并会用通项求解特定项.
 利用定积分知识求解即可.
利用定积分知识求解即可.解答:解:因为
 的展开式得通项为:Tr+1=
的展开式得通项为:Tr+1=
 •
• =(-1)r
=(-1)r •
• •2r•
•2r• •x-r;
•x-r;令
 =2⇒r=1.
=2⇒r=1.∴展开式中x2的系数为:(-1)1×
 •
• •21=-
•21=- .
.∴a=-
 .
.∴
 =
= (ex-
(ex- )dx═(ex-lnx)|
)dx═(ex-lnx)| =(e7-ln7)-(e1-ln1)=e7-ln7-e.
=(e7-ln7)-(e1-ln1)=e7-ln7-e.故答案为:e7-ln7-e.
点评:本题主要考查二项展开式的应用问题.解决问题的关键在于熟悉求二项展开式的通项,并会用通项求解特定项.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
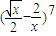 的展开式中x2的系数,则
的展开式中x2的系数,则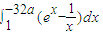 = .
= .