题目内容
一个等比数列 的前n项和为48,前2n项和为60,则前3n项和为( )
的前n项和为48,前2n项和为60,则前3n项和为( )
| A.63 | B.108 | C.75 | D.83 |
A
解析试题分析:因为等比数列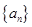 公比为
公比为 ,则
,则 仍为等比数列,其公比为
仍为等比数列,其公比为 ,根据等比数列的这一性质有48,60-48=12,
,根据等比数列的这一性质有48,60-48=12, 成等比数列,∴
成等比数列,∴ ,∴
,∴ ,故选A
,故选A
考点:本题考查了等比数列前n项和的性质
点评:熟练掌握等比数列片段和的性质是解决此类问题的关键,属基础题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在等差数列 中,公差d >0,
中,公差d >0, 是方程
是方程 的两个根,
的两个根, 是数列
是数列 的前n项的和,那么满足条件
的前n项的和,那么满足条件 >0的最小自然数n=( )
>0的最小自然数n=( )
| A.4018 | B.4017 | C.2009 | D.2010 |
已知各项均为正数的等比数列{ },
}, =5,
=5, =10,则
=10,则 =
=
A. | B.7 | C.6 | D. |
已知正项等比数列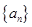 满足:
满足: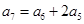 ,若存在两项
,若存在两项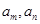 使得
使得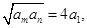 则
则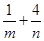 的最小值为( ).
的最小值为( ).
A.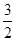 | B.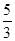 | C.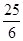 | D.不存在 |
等比数列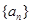 中,
中,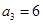 ,前三项和
,前三项和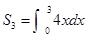 ,则公比
,则公比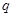 的值为
的值为
A.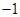 或 或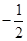 | B.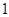 或 或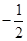 | C.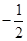 | D.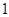 |
若{an}是等比数列,且an>0,a2a4+2a3a5+a4a6=25,则a3+a5的值为
| A.5 | B.10 | C.15 | D.20 |
设等比数列 的前项和为
的前项和为 ,若
,若 ,则
,则
| A.2 | B. | C. | D.3 |
公比为2的等比数列{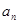 }的各项都是正数,且
}的各项都是正数,且
 =16,则
=16,则
A. | B. | C. | D. |
已知函数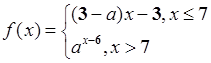 ,若数列
,若数列 满足
满足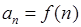 (
(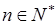 ),且
),且 是递增数列,则实数
是递增数列,则实数 的取值范围是( )
的取值范围是( )
A.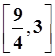 | B.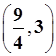 | C.(2,3) | D.(1,3) |