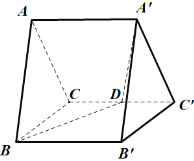
题目内容
【题目】如图,在四棱锥![]() 中,
中,![]() ,
,![]() 分别为
分别为![]() 的中点,
的中点,![]() .
.
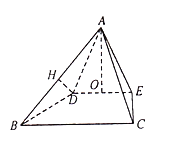
(1)求证:![]() 平面
平面![]() ;
;
(2)求直线![]() 与底面
与底面![]() 所成角的大小
所成角的大小
【答案】(1)证明见解析;(2) ![]() .
.
【解析】
(1) 取线段![]() 的中点
的中点![]() ,连接
,连接![]() ,再证明四边形
,再证明四边形![]() 为平行四边形即可.
为平行四边形即可.
(2) 连接![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() 再证明
再证明![]() 是
是![]() 与底面
与底面![]() 所成的角.再利用构造直角三角形的方法求解各边长进而求得
所成的角.再利用构造直角三角形的方法求解各边长进而求得![]() 的大小即可.
的大小即可.
(1)证明:取线段![]() 的中点
的中点![]() ,连接
,连接![]() .
.
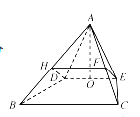
因为![]() 是
是![]() 的中位线,
的中位线,
所以![]() .
.
又因为![]() ,
,
所以![]() .
.
所以四边形![]() 为平行四边形,
为平行四边形,
所以![]() .
.
因为![]() 平面
平面![]() 平面
平面![]() .
.
所以![]() 平面
平面![]() .
.
(2)解:连接![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() .
.
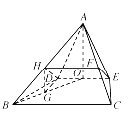
易知![]() ,
,
易知![]() 是
是![]() 的中位线,
的中位线,
所以![]() 且
且![]() .
.
因为![]() 为
为![]() 中点,
中点,![]() ,又
,又![]() ,所以
,所以![]() .
.
因为![]() ,所以
,所以![]() .
.
又![]() 平面
平面![]() ,
,
所以![]() 底面
底面![]() .
.
所以![]() 是
是![]() 与底面
与底面![]() 所成的角.
所成的角.
易求等腰梯形![]() 的高为
的高为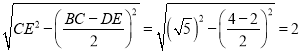
所以![]() .
.
在![]() 中,由
中,由![]() .得
.得![]() .
.
故直线![]() 与底面
与底面![]() 所成角的大小为
所成角的大小为![]() .
.

 金博士一点全通系列答案
金博士一点全通系列答案【题目】生男生女都一样,女儿也是传后人.由于某些地区仍然存在封建传统思想,头胎的男女情况可能会影响生二孩的意愿,现随机抽取某地200户家庭进行调查统计.这200户家庭中,头胎为女孩的频率为0.5,生二孩的频率为0.525,其中头胎生女孩且生二孩的家庭数为60.
(1)完成下列![]() 列联表,并判断能否有95%的把握认为是否生二孩与头胎的男女情况有关;
列联表,并判断能否有95%的把握认为是否生二孩与头胎的男女情况有关;
生二孩 | 不生二孩 | 合计 | |
头胎为女孩 | 60 | ||
头胎为男孩 | |||
合计 | 200 |
(2)在抽取的200户家庭的样本中,按照分层抽样的方法在生二孩的家庭中抽取了7户,进一步了解情况,在抽取的7户中再随机抽取4户,求抽到的头胎是女孩的家庭户数![]() 的分布列及数学期望.
的分布列及数学期望.
附:
| 0.15 | 0.05 | 0.01 | 0.001 |
| 2.072 | 3.841 | 6.635 | 10.828 |
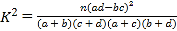 (其中
(其中![]() ).
).
【题目】响应“文化强国建设”号召,某市把社区图书阅览室建设增列为重要的民生工程.为了解市民阅读需求,随机抽取市民200人做调查,统计显示,男士喜欢阅读古典文学的有64人,不喜欢的有56人;女士喜欢阅读古典文学的有36人,不喜欢的有44人.
(1)能否在犯错误的概率不超过0.25的前提下认为喜欢阅读古典文学与性别有关系?
(2)为引导市民积极参与阅读,有关部门牵头举办市读书交流会,从这200人中筛选出5名男代表和4名代表,其中有3名男代表和2名女代表喜欢古典文学.现从这9名代表中任选3名男代表和2名女代表参加交流会,记![]() 为参加交流会的5人中喜欢古典文学的人数,求
为参加交流会的5人中喜欢古典文学的人数,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
附:![]() ,其中
,其中![]() .
.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 |