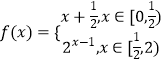Question

【题目】设y1=loga（3x+1），y2=loga（﹣3x），其中a＞0且a≠1．
（1）若y1=y2 ， 求x的值；
（2）若y1＞y2 ， 求x的取值范围．

Answer 1

【答案】
（1）解：∵y1=y2，即loga（3x+1）=loga（﹣3x），∴3x+1=﹣3x，

解得 ，

经检验3x+1＞0，﹣3x＞0，所以，x=﹣ 是所求的值

（2）解：当0＜a＜1时，∵y1＞y2，即loga（3x+1）＞loga（﹣3x），

∴ 解得 ．

当a＞1时，∵y1＞y2，即loga（3x+1）＞loga（﹣3x），

∴ 解得 ．

综上，当0＜a＜1时， ；当a＞1时，

【解析】（1）由y1=y2 ， 即loga（3x+1）=loga（﹣3x），可得3x+1=﹣3x，由此求得x的值，检验可得结论．（2）分当0＜a＜1时、和当a＞1时两种情况，分别利用对数函数的定义域及单调性，化为与之等价的不等式组，从而求得原不等式的解集．