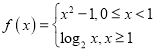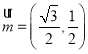题目内容
【题目】设数列![]() 的前
的前![]() 项和为
项和为![]() ,若
,若![]() ,则称
,则称![]() 是“
是“![]() 数列”.
数列”.
(1)若![]() 是“
是“![]() 数列”,且
数列”,且![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的取值范围;
的取值范围;
(2)若![]() 是等差数列,首项为
是等差数列,首项为![]() ,公差为
,公差为![]() ,且
,且![]() ,判断
,判断![]() 是否为“
是否为“![]() 数列”;
数列”;
(3)设数列![]() 是等比数列,公比为
是等比数列,公比为![]() ,若数列
,若数列![]() 与
与![]() 都是“
都是“![]() 数列”,求
数列”,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ; (2)见解析; (3)
; (2)见解析; (3)![]() .
.
【解析】
(1)根据数列的新定义,列出不等式组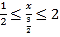 且
且![]() ,,即可求解;
,,即可求解;
(2)由等差数列![]() ,得到
,得到![]() ,进而得出
,进而得出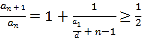 ,再由
,再由![]() 的单调性,得到
的单调性,得到![]() ,即可得到结论;
,即可得到结论;
(3)设等比数列![]() 的公比为
的公比为![]() ,分
,分![]() 和
和![]() 时,结合数列的新定义,即可作差判定.
时,结合数列的新定义,即可作差判定.
(1)由题意,数列![]() 满足
满足![]() ,称
,称![]() 是“
是“![]() 数列”,
数列”,
又由![]() ,
,![]() ,
,![]() ,
,![]() ,可得
,可得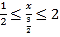 且
且![]() ,
,
解得![]() ,即
,即![]() 的取值范围是
的取值范围是![]() .
.
(2)由题意,数列![]() 的通项公式为
的通项公式为![]() ,
,
则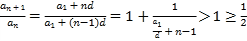 ,
,
又由![]() ,可得数列
,可得数列![]() 随着
随着![]() 的增大而减小,
的增大而减小,
所以当![]() 时,
时,![]() 取得最大值,所以
取得最大值,所以![]() ,
,
所以数列![]() 是“
是“![]() 数列”.
数列”.
(3)由题意得,等比数列![]() 的公比为
的公比为![]() ,
,
由数列![]() 是“G的数列”,可得
是“G的数列”,可得![]() ,即
,即![]() ,
,
①当![]() 时,所以
时,所以![]() ,则
,则![]() ,符合题意,
,符合题意,
②当![]() 时,则
时,则![]() ,则
,则![]() ,
,
因为数列![]() 是“G的数列”,所以
是“G的数列”,所以![]() 对
对![]() 恒成立,
恒成立,
(i)当![]() 时,
时,![]() ,
,
即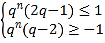 对
对![]() 恒成立,
恒成立,
因为![]() ,
,
所以![]() ,
,
所以当![]() 时,
时,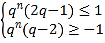 对
对![]() 恒成立;
恒成立;
(ii)当![]() 时,
时,![]() ,
,
即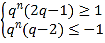 对
对![]() 恒成立,
恒成立,
因为![]() ,
,
所以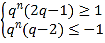 ,解得
,解得![]() ,
,
又![]() ,所以不存在
,所以不存在![]() 满足题意,
满足题意,
综上可得,数列![]() 的公比
的公比![]() 的取值范围是
的取值范围是![]() .
.

【题目】班主任为了对本班学生的考试成绩进行分析,决定从本班24名女同学,18名男同学中随机抽取一个容量为7的样本进行分析.
(1)如果按照性别比例分层抽样,可以得到多少个不同的样本?(写出算式即可,不必计算出结果)
(2)如果随机抽取的7名同学的数学,物理成绩(单位:分)对应如下表:
学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
数学成绩 | 60 | 65 | 70 | 75 | 85 | 87 | 90 |
物理成绩 | 70 | 77 | 80 | 85 | 90 | 86 | 93 |
①若规定85分以上(包括85分)为优秀,从这7名同学中抽取3名同学,记3名同学中数学和物理成绩均为优秀的人数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
②根据上表数据,求物理成绩![]() 关于数学成绩
关于数学成绩![]() 的线性回归方程(系数精确到0.01);若班上某位同学的数学成绩为96分,预测该同学的物理成绩为多少分?
的线性回归方程(系数精确到0.01);若班上某位同学的数学成绩为96分,预测该同学的物理成绩为多少分?
附:线性回归方程![]() ,
,
其中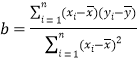 ,
,![]() .
.
|
|
|
|
76 | 83 | 812 | 526 |