Question

【题目】如图，以坐标原点O为圆心的单位圆与x轴正半轴相交于点A，点B，P在单位圆上，且B（﹣ ， ），∠AOB=α．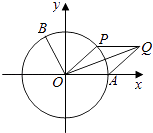

（1）求 的值；
（2）设∠AOP=θ（ ≤θ≤ π）， = + ，四边形OAQP的面积为S，f（θ）=（ ﹣1）2+ S﹣1，求f（θ）的最值及此时θ的值．

Answer 1

【答案】
（1）解：依题意，tanα= =﹣2，

∴ = = =﹣10

（2）解：由已知点P的坐标为P（cosθ，sinθ），

又 = + ， ，

∴四边形OAQP为菱形，

∴S=2S△OAP=sinθ，

∵A（1，0），P（cosθ，sinθ），

∴ =（1+cosθ，sinθ），

∴ =1+cosθ，

∴f（θ）=（1+cosθ﹣1）2+ sinθ﹣1

=cos2θ+ sinθ﹣1

=﹣sin2θ+ sinθ，

∵ ≤sinθ≤1，

∴当sinθ= ，即θ= 时，f（θ）max= ；

当sinθ=1，即θ= 时，f（θ）max= ﹣1

【解析】（1）依题意，可求得tanα=2，将 中的“弦”化“切”即可求得其值；（2）利用向量的数量积的坐标运算可求得f（θ）=﹣sin2θ+ sinθ；θ∈[ ， ] ≤sinθ≤1，利用正弦函数的单调性与最值即可求得f（θ）的最值及此时θ的值．