题目内容
20.已知函数f(x)=9x+1.(1)若g(x)=f(x4)-37,求g(x)的解析式;
(2)求函数g(x)的零点.
分析 (1)由题意可得g(x)=9x4-36;
(2)令g(x)=9x4-36=0,解方程可得解,可得零点.
解答 解:(1)∵f(x)=9x+1,
∴g(x)=f(x4)-37=9x4-36;
(2)令g(x)=9x4-36=0,
解方程可得x4=4,x=±$\sqrt{2}$,
∴函数g(x)的零点为±$\sqrt{2}$.
点评 本题考查函数解析式的求解,涉及函数的零点,属基础题.

练习册系列答案
相关题目
10.设函数$f(x)=\left\{\begin{array}{l}(a-2)x,(x≤2)\\{2^x}-1,(x>2)\end{array}\right.$是R上的单调递增函数,则实数a的取值范围为( )
| A. | (2,+∞) | B. | (-∞,$\frac{7}{2}$] | C. | (2,$\frac{7}{2}$) | D. | (2,$\frac{7}{2}]$ |
11.某产品广告费x(千元)与销售额y(万元)之间有如图对应数据:
(1)求销售额y关于广告费x的线性回归方程$\widehat{y}$=bx+a;
(2)当广告费支出1万元时,预测销售额为多少万元?
(参考公式:b=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,a=$\overline{y}$-b$\overline{x}$)
| x | 2 | 4 | 5 | 6 | 8 |
| y | 3 | 4 | 6 | 5 | 7 |
(2)当广告费支出1万元时,预测销售额为多少万元?
(参考公式:b=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,a=$\overline{y}$-b$\overline{x}$)
8.过点(-a-6,3),(2a,3a)的直线与过点点(2,1),(3,1)的直线垂直,则实数a的值是( )
| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
9.点A(-3,6)关于点P(2,-1)对称点的点的坐标是( )
| A. | (1,-4) | B. | (1,4) | C. | (-7,8) | D. | (7,-8) |
18.圆心在抛物线y2=2x(y>0)上,并且与抛物线的准线及x轴都相切的方程是( )
| A. | x2+y2-x-2y-$\frac{1}{4}$=0, | B. | x2+y2+x-2y+1=0, | ||
| C. | x2+y2-x+1=0, | D. | x2+y2-x-2y+$\frac{1}{4}$=0, |
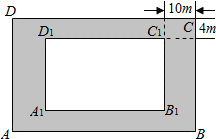 如图,某房地产开发公司计划在一楼区内建造一个长方形公园ABCD,公园由长方形的休闲区A1B1C1D1和环公园人行道(阴影部分)组成,已知人行道的宽分别为4m和10m
如图,某房地产开发公司计划在一楼区内建造一个长方形公园ABCD,公园由长方形的休闲区A1B1C1D1和环公园人行道(阴影部分)组成,已知人行道的宽分别为4m和10m