题目内容
(本题满分12分)已知双曲线 及点
及点 ,是否存在过点
,是否存在过点 的直线
的直线 ,使直线
,使直线 被双曲线截得的弦恰好被
被双曲线截得的弦恰好被 点平分?若存在,求出直线
点平分?若存在,求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
不存在.
【解析】
试题分析:存在性问题常先假设存在,如果最终无解或矛盾,则假设不成立,得出结论.一般地,解决弦长问题的常用方法是把直线方程和双曲线方程组成方程组,消元后转化成关于x(或y)的一元二次方程,利用根与系数的关系及整体代入的思想解题.设直线与双曲线交于A(x1,y1),B(x2,y2)两点,直线的斜率为k,则|AB|=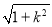 |x1-x2|.与中点有关的问题常用“点差法”来解.本题涉及到中点故用点差法,但要注意点差法求解时要带回验证.
|x1-x2|.与中点有关的问题常用“点差法”来解.本题涉及到中点故用点差法,但要注意点差法求解时要带回验证.
试题解析:假设符合题意的直线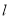 存在. 1分
存在. 1分
设直线l与双曲线的两个交点分别为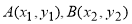 .
.
∴ 5分
5分
∵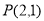 为
为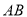 的中点,
的中点,
∴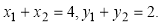 7分
7分
∴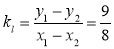 . 8分
. 8分
∴直线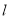 的方程为
的方程为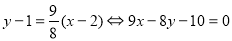 10分
10分
由过p与双曲线有两个焦点时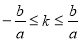 即
即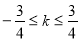 11分
11分
∴不存在符合题意的直线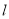 . 12分
. 12分
考点:双曲线、直线的位置关系的综合应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 B.
B. C.
C. D.
D.
 的图象是下面图中的( )
的图象是下面图中的( )



 ,若函数
,若函数 ,则
,则 的解集为( )
的解集为( ) B.
B. C.
C. D.
D.
 到集合
到集合 的函数的是 ( )
的函数的是 ( ) ,
, ,对应法则
,对应法则
 圆
圆 上的点
上的点
 ,
, 圆
圆 ,对应法则:过
,对应法则:过 ,对应法则
,对应法则 ,
,
 为非零整数
为非零整数 ,
, ,对应法则
,对应法则
 上,并且经过圆
上,并且经过圆 与圆
与圆





 交点的圆的方程为 .
交点的圆的方程为 . 与曲线
与曲线 有公共点,则
有公共点,则 的取值范围是
的取值范围是 B.
B. C
C  D
D 
 的焦点为
的焦点为 ,过
,过 的直线,与抛物线交于
的直线,与抛物线交于 两点,若
两点,若 ,则
,则 =( )
=( ) B.
B. C.
C. D.
D.
