题目内容
数列{an}中，a1=
，前n项和Sn满足Sn+1-Sn=（
）n+1（n∈N*）．
（Ⅰ）求数列{an}的通项公式an以及前n项和Sn；
（Ⅱ）若S1，t（S1+S2），3（S2+S3）成等差数列，求实数t的值．
| 1 |
| 3 |
| 1 |
| 3 |
（Ⅰ）求数列{an}的通项公式an以及前n项和Sn；
（Ⅱ）若S1，t（S1+S2），3（S2+S3）成等差数列，求实数t的值．
（Ⅰ）由Sn+1-Sn=（
）n+1得an+1=(
)n+1（n∈N*）；
又a1=
，故an=(
)n（n∈N*）
从而sn=
=
[1-(
)n]（n∈N*）．
（Ⅱ）由（Ⅰ）可得S1=
，S2=
，S3=
．
从而由S1，t（S1+S2），3（S2+S3）成等差数列可得：
+3×(
+
)=2×(
+
)t，解得t=2．
| 1 |
| 3 |
| 1 |
| 3 |
又a1=
| 1 |
| 3 |
| 1 |
| 3 |
从而sn=
| ||||
1-
|
| 1 |
| 2 |
| 1 |
| 3 |
（Ⅱ）由（Ⅰ）可得S1=
| 1 |
| 3 |
| 4 |
| 9 |
| 13 |
| 27 |
从而由S1，t（S1+S2），3（S2+S3）成等差数列可得：
| 1 |
| 3 |
| 4 |
| 9 |
| 13 |
| 27 |
| 1 |
| 3 |
| 4 |
| 9 |
练习册系列答案
相关题目
___________.
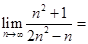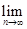
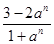的值是 .
。