题目内容
已知a、b、c∈(0,+∞),且a+b+c=1,则(a+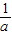 )+(b+
)+(b+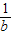 )+(c+
)+(c+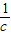 )的最小值为 .
)的最小值为 .
【答案】分析:把1=a+b+c代入要求的式子,再利用基本不等式的性质即可求出最小值.
解答:解:∵a、b、c∈(0,+∞),(a+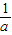 )+(b+
)+(b+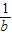 )+(c+
)+(c+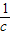 )=(a+
)=(a+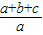 )+(b+
)+(b+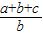 )+(c+
)+(c+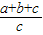 )
)
=4+(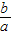 +
+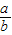 )+(
)+(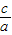 +
+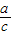 )+(
)+(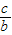 +
+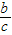 )≥4+2+2+2=10,当且仅当a=b=c=
)≥4+2+2+2=10,当且仅当a=b=c= 时取等号.
时取等号.
∴(a+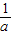 )+(b+
)+(b+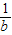 )+(c+
)+(c+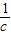 )的最小值10.
)的最小值10.
故答案为10.
点评:把1代入要求的式子及利用基本不等式的性质是解题的关键.
解答:解:∵a、b、c∈(0,+∞),(a+
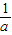 )+(b+
)+(b+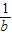 )+(c+
)+(c+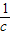 )=(a+
)=(a+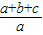 )+(b+
)+(b+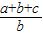 )+(c+
)+(c+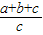 )
)=4+(
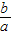 +
+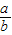 )+(
)+(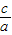 +
+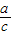 )+(
)+(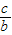 +
+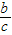 )≥4+2+2+2=10,当且仅当a=b=c=
)≥4+2+2+2=10,当且仅当a=b=c= 时取等号.
时取等号.∴(a+
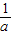 )+(b+
)+(b+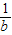 )+(c+
)+(c+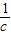 )的最小值10.
)的最小值10.故答案为10.
点评:把1代入要求的式子及利用基本不等式的性质是解题的关键.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案
相关题目
已知a,b,c∈(0,+∞),3a-2b+c=0,则
的( )
| ||
| b |
A、最大值是
| ||||
B、最小值是
| ||||
C、最大值是
| ||||
D、最小值是
|
已知a>b>c>0,若P=
,Q=
,则( )
| b-c |
| a |
| a-c |
| b |
| A、P≥Q | B、P≤Q |
| C、P>Q | D、P<Q |