题目内容

圆x²+y²+Dx+Ey+F=0关于直线l₁：x-y+4=0与直线l₂：x+3y=0都对称，则D=，E=．

6 -2
分析：由圆关于两直线都对称，得到两直线都过圆心，即两直线交点为圆心，联立两直线方程求出交点坐标，确定出圆心坐标，利用圆心坐标公式即可求出D与E的值．
解答：由题设知直线l₁，l₂的交点为已知圆的圆心，
由 $\text{[math]}$ ，得到 $\text{[math]}$ ，
∴圆心坐标为（-3，1），
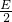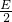∴- $\text{[math]}$ =-3，- $\text{[math]}$ =1，
则D=6，E=-2．
故答案为：6；-2
点评：此题考查了直线与圆的位置关系，以及关于点、直线对称的圆的方程，根据题意得到两直线的交点即为圆心是解本题的关键．

练习册系列答案

一通百通小学毕业升学模拟测试卷系列答案

真题集训小学期末全程测试卷系列答案

100分闯关考前冲刺全真模拟系列答案

启航学期总动员系列答案

全国历届中考真题分类一卷通系列答案

考卷王单元检测评估卷系列答案

心算口算巧算一课一练系列答案

典元教辅小学毕业升学必备小升初押题卷系列答案

金榜夺冠真题卷系列答案

小升初综合素质检测卷系列答案

相关题目

已知圆x²+y²+Dx+Ey=0的圆心在直线x+y=l上则D与E的关系是（　　）

下面给出的四个命题中：
①对任意的n∈N*，点P_n（n，a_n）都在直线y=2x+1上是数列a_n为等差数列的充分不必要条件；
②“m=-2”是直线（m+2）x+my+1=0与“直线（m-2）x+（m+2）y-3=0相互垂直”的必要不充分条件；
③设圆x²+y²+Dx+Ey+F=0（D²+E²-4F＞0）与坐标轴有4个交点A（x₁，0），B（x₂，0），C（0，y₁），D（0，y₂），则有x₁x₂-y₁y₂=0；
④将函数y=cos2x的图象向右平移

个单位，得到函数y=sin(2x-

)的图象．
其中是真命题的有

（将你认为正确的序号都填上）．

圆x²+y²+Dx+Ey+F=0（D²+E²-4F＞0）关于直线x-y=0对称，则（　　）

（2013•济宁二模）下列命题：
①线性回归方程对应的直线

至少经过其样本数据点（x₁，y_l），（x₁，y_l），…，（x_n，y_n）中的一个点；
②设f（x）为定义在R上的奇函数，当x＞0时，f（x）=

．则当x＜0时，f（x）=

；
③若圆x²+y²+Dx+Ey+F=0（D²+E²-4F＞0）与坐标轴的交点坐标分别为（x₁，0），（x₂，0），（0，y_l），（0，y₂），则x₁x₂-y₁y₂=0；
④若圆锥的底面直径为2，母线长为

，则该圆锥的外接球表面积为4π．
其中正确命题的序号为．

．（把所有正确命题的序号都填上）

已知圆x²+y²+Dx+Ey+F=0的圆心在y轴上，则必有（　　）

D、D=0，且E=0