题目内容
对 ﹣﹣﹣﹣﹣﹣﹣大前提,
﹣﹣﹣﹣﹣﹣﹣大前提,
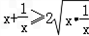 ,﹣﹣﹣﹣﹣﹣小前提,
,﹣﹣﹣﹣﹣﹣小前提,
所以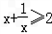 ,﹣﹣﹣﹣﹣﹣﹣结 论,
,﹣﹣﹣﹣﹣﹣﹣结 论,
以上推理过程中的错误为( )
(1)大前提 (2)小前提 (3)结论 (4)无错误.
 ﹣﹣﹣﹣﹣﹣﹣大前提,
﹣﹣﹣﹣﹣﹣﹣大前提,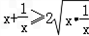 ,﹣﹣﹣﹣﹣﹣小前提,
,﹣﹣﹣﹣﹣﹣小前提,所以
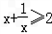 ,﹣﹣﹣﹣﹣﹣﹣结 论,
,﹣﹣﹣﹣﹣﹣﹣结 论,以上推理过程中的错误为( )
(1)大前提 (2)小前提 (3)结论 (4)无错误.
(2)(3)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
 ﹣﹣﹣﹣﹣﹣﹣大前提,
﹣﹣﹣﹣﹣﹣﹣大前提,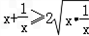 ,﹣﹣﹣﹣﹣﹣小前提,
,﹣﹣﹣﹣﹣﹣小前提,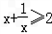 ,﹣﹣﹣﹣﹣﹣﹣结 论,
,﹣﹣﹣﹣﹣﹣﹣结 论,
 阅读快车系列答案
阅读快车系列答案