Question

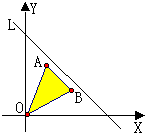
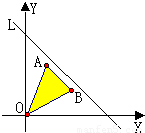
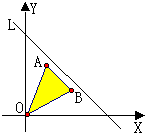如图，已知原点O及点A（1，2），B（a，1），若图中阴影部分（包括边界）上所有的点都在不等式x+y≤4所表示的平面区域内，则实数a的范围是

1. A.
   a≤4
2. B.
   a≤3
3. C.
   a≤2
4. D.
   a≥3

Answer 1

B
分析：欲使得阴影部分（包括边界）上所有的点都在不等式x+y≤4所表示的平面区域内，只须点B在不等式x+y≤4所表示的平面区域内即可．根据点（a，1）在不等式x+y≤4所表示的平面区域内，将点的坐标代入，列出关于a的不等式，求出实数a的取值范围．
解答：由题意知，B在不等式x+y≤4所表示的平面区域内，
点（a，1）在不等式x+y≤4所表示的平面区域内，
根据二元一次不等式（组）与平面区域可知：
a+1≤4
所以a≤3，
则实数a的取值范围是a≤3．
故选B．
点评：考查二元一次不等式（组）与平面区域，理解二元一次不等式表示的平面区域，会利用数形结合的数学思想解决问题．