题目内容
设数列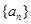 的前
的前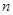 项和为
项和为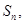 已知
已知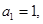
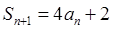
(I)设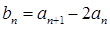 ,证明数列
,证明数列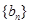 是等比数列;
是等比数列;
(II)求数列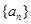 的通项公式.
的通项公式.
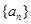 的前
的前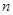 项和为
项和为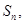 已知
已知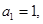
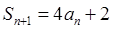
(I)设
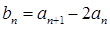 ,证明数列
,证明数列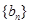 是等比数列;
是等比数列; (II)求数列
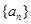 的通项公式.
的通项公式.
(I)见解析;(II)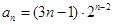 。
。
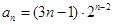 。
。此题主要考查了等比数列的性质及其前n项和,运用了错位相减法求数列{an}的前n项和,这个方法是高考中常用的方法,同学们要熟练掌握它
(Ⅰ)由题意只要证明bnbn-1
为一常数即可,已知Sn+1=4an+1,推出b1的值,然后继续递推相减,得an+1-2an=2(an-2an-1),从而求出bn与bn-1的关系;
(Ⅱ)根据(Ⅰ){bn}是等比数列,可得bn}的通项公式,从而证得数列{an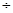 2n }是首项为1
2n }是首项为1 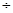 2 ,公差为1 2 的等差数列,最后利用错位相减法,求出数列{an}的通项公式
2 ,公差为1 2 的等差数列,最后利用错位相减法,求出数列{an}的通项公式
解:(I)由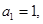 及
及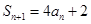 ,有
,有
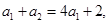

由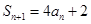 ,...① 则当
,...① 则当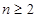 时,有
时,有 .....②
.....②
②-①得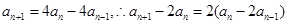
又 ,
,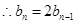
 是首项
是首项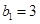 ,公比为2的等比数列.
,公比为2的等比数列.
(II)由(I)可得 ,
,
 数列
数列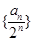 是首项为
是首项为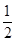 ,公差为
,公差为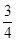 的等差数列.
的等差数列.
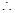
 ,
,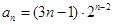
(Ⅰ)由题意只要证明bnbn-1
为一常数即可,已知Sn+1=4an+1,推出b1的值,然后继续递推相减,得an+1-2an=2(an-2an-1),从而求出bn与bn-1的关系;
(Ⅱ)根据(Ⅰ){bn}是等比数列,可得bn}的通项公式,从而证得数列{an
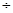 2n }是首项为1
2n }是首项为1 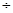 2 ,公差为1 2 的等差数列,最后利用错位相减法,求出数列{an}的通项公式
2 ,公差为1 2 的等差数列,最后利用错位相减法,求出数列{an}的通项公式解:(I)由
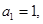 及
及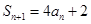 ,有
,有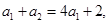

由
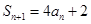 ,...① 则当
,...① 则当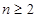 时,有
时,有 .....②
.....②②-①得
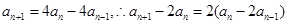
又
 ,
,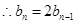
 是首项
是首项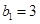 ,公比为2的等比数列.
,公比为2的等比数列.(II)由(I)可得
 ,
,
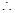 数列
数列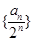 是首项为
是首项为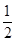 ,公差为
,公差为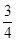 的等差数列.
的等差数列.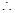
 ,
,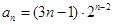

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
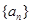 满足
满足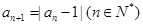 ,
,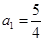 ,求
,求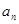 ;
;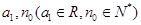 ,使当
,使当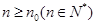 时,
时,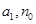 ,否则说明理由;
,否则说明理由; 的等比数列{
的等比数列{ }的前
}的前 项和为
项和为 ,若
,若 ,
,  =________.
=________. 的公比不为1的等比数列,且
的公比不为1的等比数列,且 成等差数列。
成等差数列。 ,求数列
,求数列 的前
的前 项和
项和 .
.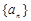 中,若公比
中,若公比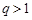 ,且
,且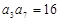 ,
,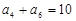 ,则
,则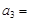
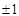
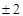
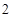
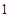
 的公比为正数,且
的公比为正数,且 ,
, ,则
,则 ( )
( )

 的公比为正数,且
的公比为正数,且 则
则


 的各项均为正数,且
的各项均为正数,且 ,则
,则 ( )
( )
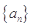 中,
中,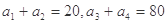 ,则
,则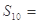 __________
__________