题目内容
设函数f(x)＝x2＋
(x≠0)．当a>1时，方程f(x)＝f(a)的实根个数为________．
3
解析 令g(x)＝f(x)－f(a)，即g(x)＝x2＋－a2－
，
整理得：g(x)＝
(x－a)(ax2＋a2x－2)．
显然g(a)＝0，令h(x)＝ax2＋a2x－2.
∵h(0)＝－2<0，h(a)＝2(a3－1)>0，
∴h(x)在区间(－∞，0)和(0，a)各有一个零点．
因此，g(x)有三个零点，即方程f(x)＝f(a)有三个实数解．
练习册系列答案
53随堂测系列答案
相关题目
上的一点向圆
引切线，则切线长的
C．
D．3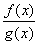
＝ax，且f′(x)g(x)<f(x)g′(x)，
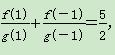，若有穷数列
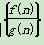(n∈N*)的前n项和等于
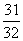，则n等于( )
(a>0)的展开式中常数项为240，则(x＋a)(x－2a)2的展开式中x2项的系数为________．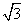
cos(2x＋φ)＋sin(2x＋φ)
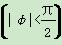，且其图象关于直线x＝0对称，则( )
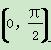上为增函数
上为增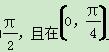函数
上为减函数
＋3
|的最小值为________．
，若
，则
的值为 
，则实数
的取值范围是
.