题目内容
已知 1≤log2x≤2
(1)求f(x)=x2+2x+3的最小值;
(2)求g(x)=log2
•log2
的值域.
(1)求f(x)=x2+2x+3的最小值;
(2)求g(x)=log2
| x |
| 4 |
| x |
| 2 |
分析:(1)确定x的范围,利用配方法,确定函数的单调性,即可求f(x)=x2+2x+3的最小值;
(2)利用换元法,再进行配方,即可求得函数的值域.
(2)利用换元法,再进行配方,即可求得函数的值域.
解答:解:(1)∵1≤log2x≤2,∴2≤x≤4
∵f(x)=x2+2x+3=(x+1)2+2
∴函数在[2,4]上单调递增
∴f(x)=x2+2x+3的最小值为f(2)=11;
(2)g(x)=log2
•log2
=(log2x-2)(log2x-1)
设t=log2x,则1≤t≤2,y=t2-3t+2=(t-
)2-
∵1≤t≤2,∴t=
,即x=2
时,ymin=-
t=1或t=2,即x=2或4时,ymax=0
∴g(x)=log2
•log2
的值域为[-
,0].
∵f(x)=x2+2x+3=(x+1)2+2
∴函数在[2,4]上单调递增
∴f(x)=x2+2x+3的最小值为f(2)=11;
(2)g(x)=log2
| x |
| 4 |
| x |
| 2 |
设t=log2x,则1≤t≤2,y=t2-3t+2=(t-
| 3 |
| 2 |
| 1 |
| 4 |
∵1≤t≤2,∴t=
| 3 |
| 2 |
| 2 |
| 1 |
| 4 |
t=1或t=2,即x=2或4时,ymax=0
∴g(x)=log2
| x |
| 4 |
| x |
| 2 |
| 1 |
| 4 |
点评:本题考查函数的最值,考查函数的值域,考查配方法的运用,属于中档题.

练习册系列答案
相关题目
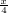 •log2
•log2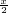 的值域.
的值域.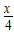 •log2
•log2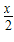 的值域.
的值域.