题目内容
下列函数中，随x的增大而增大速度最快的是（ ）
分析：根据指数函数y=ax（a＞1）、对数函数y=logax（a＞1）和一次函数y=kx（k＞0）的图象与性质，将各选项中的函数加以比较，即可得到增大速度最快的函数．
解答：解：
通过函数y=ax（a＞1）、y=logax（a＞1）和y=kx（k＞0）的图象，
观察可得y=ax的增大速度要比y=kx增大速度快，y=kx的增大速度又要比y=logax的增大速度快，
因此可得A、D两项的函数增大速度要快于B、C两项的函数
又∵函数y=
ex中，底数e=2.71828…，
函数y=100•2x中，底数为2，且e＞2
∴函数y=
ex的函数的增大速度要快于函数y=100•2x增大速度
故选：A
通过函数y=ax（a＞1）、y=logax（a＞1）和y=kx（k＞0）的图象，观察可得y=ax的增大速度要比y=kx增大速度快，y=kx的增大速度又要比y=logax的增大速度快，
因此可得A、D两项的函数增大速度要快于B、C两项的函数
又∵函数y=
| 1 |
| 100 |
函数y=100•2x中，底数为2，且e＞2
∴函数y=
| 1 |
| 100 |
故选：A
点评：本题给出几个基本初等函数，求其中的增长速度最快的函数．着重考查了指数函数、对数函数和一次函数的图象与性质等知识，属于基础题．
练习册系列答案
相关题目
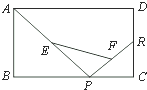已知矩形ABCD，R、P分别在边CD、BC上，E、F分别为AP、PR的中点，当P在BC上由B向C运动时，点R在CD上固定不变，设BP=x，EF=y，那么下列结论中正确的是（ ）| A、y是x的增函数 | B、y是x的减函数 | C、y随x先增大后减小 | D、无论x怎样变化，y是常数 |
