题目内容
已知函数f（x）=x3（x＞0），点An（n，yn），An+1（n+1，yn+1）在函数f（x）的图象上（n∈N*）过点An，An+1的切线分别为Ln，Ln+1，Ln与Ln+1的交点的横坐标为xn．设
，则
=
- A.
- B.1
- C.
- D.
A
分析：先求出其导函数，进而得到在点An，An+1的切线方程，根据函数值相等求出Ln与Ln+1的交点的横坐标xn的表达式；进而求出an的表达式，通过对其分离常数以及裂项即可求出答案．
解答：对y=x3（n∈N*）求导得y′=3x2，
令x=n得在点An（n，yn）处的切线的斜率k=3n2，
所以在点An（n，yn）处的切线方程为y-n3=k（x-n）=3n2（x-n）?y=3n2x-2n3；
同理在An+1的切线方程为：y-（n+1）3=3（n+1）2[x-（n+1）]?y=3（n+1）2x-2（n+1）3．
∴3n2x-2n3=3（n+1）2x-2（n+1）3?x=
即
?xn-1=
．
∴=
•
=
=
=+
=+
（
）．
∴=
=
=（+
×
）
=．
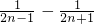故选：A．
点评：本小题主要考查直线的斜率、利用导数研究曲线上某点切线方程、数列的分组求和，裂项相消等基础知识，考查运算求解能力、化归与转化思想．属于基础题．
分析：先求出其导函数，进而得到在点An，An+1的切线方程，根据函数值相等求出Ln与Ln+1的交点的横坐标xn的表达式；进而求出an的表达式，通过对其分离常数以及裂项即可求出答案．
解答：对y=x3（n∈N*）求导得y′=3x2，
令x=n得在点An（n，yn）处的切线的斜率k=3n2，
所以在点An（n，yn）处的切线方程为y-n3=k（x-n）=3n2（x-n）?y=3n2x-2n3；
同理在An+1的切线方程为：y-（n+1）3=3（n+1）2[x-（n+1）]?y=3（n+1）2x-2（n+1）3．
∴3n2x-2n3=3（n+1）2x-2（n+1）3?x=
即
?xn-1=．∴
=•===+=+（）．∴
==
=（+×）=
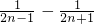．故选：A．
点评：本小题主要考查直线的斜率、利用导数研究曲线上某点切线方程、数列的分组求和，裂项相消等基础知识，考查运算求解能力、化归与转化思想．属于基础题．
练习册系列答案
相关题目
已知函数f（x）=Asin（ωx+φ）（x∈R，A＞0，ω＞0，|φ|＜| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|