题目内容
已知函数f(x)=x(
+
)
①求函数f(x)的定义域;
②判断函数f(x)的奇偶性并证明你的结论.
| 1 |
| 2x-1 |
| 1 |
| 2 |
①求函数f(x)的定义域;
②判断函数f(x)的奇偶性并证明你的结论.
考点:函数奇偶性的判断
专题:函数的性质及应用
分析:(1)由已知,2x-1≠0,得x≠0,从而求出函数的定义域;
(2)判断f(-x)和f(x)的关系,又由(1),f(x)的定义域关于原点对称,从而得到函数的奇偶性.
(2)判断f(-x)和f(x)的关系,又由(1),f(x)的定义域关于原点对称,从而得到函数的奇偶性.
解答:
解:(1)由已知,2x-1≠0,得x≠0,
∴函数f(x)的定义域为{x|x∈R且x≠0};
(2)函数f(x)=x(
+
)是偶函数,
∵f(-x)=-x(
+
)
=x(
+
),
∴f(-x)=f(x),
又由(1),f(x)的定义域关于原点对称,
∴函数f(x)=x(
+
)是偶函数.
∴函数f(x)的定义域为{x|x∈R且x≠0};
(2)函数f(x)=x(
| 1 |
| 2x-1 |
| 1 |
| 2 |
∵f(-x)=-x(
| 2x |
| 1-2x |
| 1 |
| 2 |
=x(
| 1 |
| 2x-1 |
| 1 |
| 2 |
∴f(-x)=f(x),
又由(1),f(x)的定义域关于原点对称,
∴函数f(x)=x(
| 1 |
| 2x-1 |
| 1 |
| 2 |
点评:本题考查了函数的奇偶性,利用奇偶性的定义判断即可,本题是一道基础题.

练习册系列答案
相关题目
已知m、n是两条不同的直线,α、β是两个不同的平面,则下列命题正确的是( )
| A、若m∥n,m∥α,则n∥α |
| B、若m⊥α,n⊥α,则m∥n |
| C、若n⊥α,m⊥β,则m⊥n |
| D、若α∥β,n⊥β,则m⊥α |
函数y=x2+x
是( )
| 1 |
| 2 |
| A、偶函数 | B、奇函数 |
| C、既奇既偶 | D、非奇非偶 |
若点O和点F分别为椭圆
+y2=1的中心和右焦点,点P为椭圆上的任意一点,则
•
的最小值为( )
| x2 |
| 2 |
| OP |
| FP |
A、2-
| ||
B、
| ||
C、2+
| ||
| D、1 |
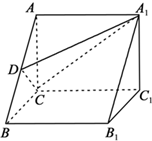 如图,在三棱柱ABC-A1B1C1中,AC⊥BC,AB⊥BB1,AC=BC=BB1=2,D为AB的中点,且CD⊥DA1.
如图,在三棱柱ABC-A1B1C1中,AC⊥BC,AB⊥BB1,AC=BC=BB1=2,D为AB的中点,且CD⊥DA1. 如图是某中学高二年级举办的演讲比赛上,七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的中位数为
如图是某中学高二年级举办的演讲比赛上,七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的中位数为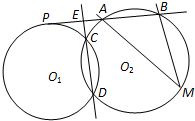 已知⊙O1和⊙O2交于点C和D,⊙O1上的点P处的切线交⊙O2于A、B点,交直线CD于点E,M是⊙O2上的一点,若PE=2,EA=1,∠AMB=45°,那么⊙O2的半径为
已知⊙O1和⊙O2交于点C和D,⊙O1上的点P处的切线交⊙O2于A、B点,交直线CD于点E,M是⊙O2上的一点,若PE=2,EA=1,∠AMB=45°,那么⊙O2的半径为