题目内容
6.已知函数f(x)满足以下条件:①f(x)=2f(x-2);②当x∈[-1,1]时,f(x)=|x|-1.(1)当x∈[-1,5]时,求函数y=f(x)+$\frac{1}{2}$的零点构成的集合;
(2)当x∈[-7,0]∪(0,7)时,利用图象法判断函数y=f(x)-log${\;}_{\frac{1}{3}}$|x|的零点个数.
分析 (1)求出当x∈[-1,5]时,函数f(x)的解析式,由函数y=f(x)+$\frac{1}{2}$=0,解方程即可;
(2)由y=f(x)-log${\;}_{\frac{1}{3}}$|x|=0得f(x)=log${\;}_{\frac{1}{3}}$|x|,分别作出两个函数的图象,利用数形结合即可得到结论.
解答 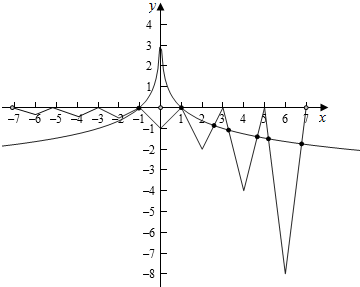 解:(1)由y=f(x)+$\frac{1}{2}$=0得f(x)=-$\frac{1}{2}$,
解:(1)由y=f(x)+$\frac{1}{2}$=0得f(x)=-$\frac{1}{2}$,
①当x∈[-1,1]时,由f(x)=|x|-1=-$\frac{1}{2}$得|x|=$\frac{1}{2}$.
则x=$\frac{1}{2}$或-$\frac{1}{2}$,
②若1≤x≤3,则-1≤x-2≤1,
即f(x)=2f(x-2)=2(|x-2|-1)=2|x-2|-2,x∈[1,3],
由f(x)=-$\frac{1}{2}$,得f(x)=2|x-2|-2=-$\frac{1}{2}$,即|x-2|=$\frac{3}{4}$,解得x=$\frac{5}{4}$或$\frac{11}{4}$.
③若3≤x≤5,则1≤x-2≤3,
即f(x)=2f(x-2)=2(2|x-4|-2)=4|x-4|-4,x∈[3,5],
由f(x)=-$\frac{1}{2}$,得f(x)=4|x-4|-4=-$\frac{1}{2}$,即|x-4|=$\frac{7}{8}$,解得x=$\frac{25}{8}$或$\frac{39}{8}$.
即当x∈[-1,5]时,求函数y=f(x)+$\frac{1}{2}$的零点构成的集合为{$\frac{1}{2}$,-$\frac{1}{2}$,$\frac{5}{4}$,$\frac{11}{4}$,$\frac{25}{8}$,$\frac{39}{8}$}.
(2)由y=f(x)-log${\;}_{\frac{1}{3}}$|x|=0得f(x)=log${\;}_{\frac{1}{3}}$|x|,
根据条件作出函数f(x)在[-7,0]∪(0,7)上的图象如图,作出y=log${\;}_{\frac{1}{3}}$|x|,
由图象知,两个函数在[-7,0]∪(0,7)上的交点个数为7个,
故函数y=f(x)-log${\;}_{\frac{1}{3}}$|x|的零点个数为7个.
点评 本题主要考查函数零点和方程的应用,利用数形结合是解决本题的关键.综合性较强,有一定的难度.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| 工作代码 | 紧前工作 | 工期(天) |
| A | 无 | 7 |
| B | 无 | 3 |
| C | 无 | 1 |
| D | C | 3 |
| E | A,B,D | 3 |
| F | E | 2 |
| G | A,B,D | 2 |
| H | F,G | 1 |
(2)指出关键路径;
(3)确定完成工程的最短总工期.
| A. | (1,2) | B. | (2,2) | C. | (0,2) | D. | (-1,2) |
| A. | y=x-x2 | B. | y=|x+1| | C. | y=-$\frac{1}{x}$ | D. | y=x2-2x |