题目内容
设函数 ,给出下列三个论断:
,给出下列三个论断:①f(x)的图象关于直线
 对称;
对称;②f(x)的周期为π;
③f(x)的图象关于点
 对称.
对称.以其中的两个论断为条件,余下的一个论断作为结论,写出你认为正确的一个命题,并对该命题加以证明.
【答案】分析:分析知,为求ω,必须有②,又有①与条件 可解得,∅=-
可解得,∅=- ,由此得f(x)=sin(2x-
,由此得f(x)=sin(2x- ),进行验证知f(x)的图象关于点
),进行验证知f(x)的图象关于点 对称,由此知
对称,由此知 .
.
解答:解: ,证明如下.
,证明如下.
由②知ω=2,故f(x)=sin(2x+φ)
又f(x)的图象关于直线 对称
对称
故sin(- +φ)=±1
+φ)=±1
- +φ=2kπ±
+φ=2kπ± ,k∈Z
,k∈Z
又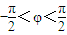 ,对k赋值知,∅=-
,对k赋值知,∅=-
故f(x)=sin(2x- )
)
令f(x)=sin(2x- )=0
)=0
可得2x- =kπ,k∈Z
=kπ,k∈Z
故有x=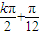 ,k∈Z,即对称中心的坐标是(
,k∈Z,即对称中心的坐标是( ,0)
,0)
当k=0时,可知f(x)的图象关于点 对称.
对称.
故
点评:本题考点是由y=Asin(ωx+φ)的部分图象确定其解析式,在新教材的高考中,这种开放式答案不唯一的题近几年有增多的趋势.
 可解得,∅=-
可解得,∅=- ,由此得f(x)=sin(2x-
,由此得f(x)=sin(2x- ),进行验证知f(x)的图象关于点
),进行验证知f(x)的图象关于点 对称,由此知
对称,由此知 .
.解答:解:
 ,证明如下.
,证明如下.由②知ω=2,故f(x)=sin(2x+φ)
又f(x)的图象关于直线
 对称
对称故sin(-
 +φ)=±1
+φ)=±1-
 +φ=2kπ±
+φ=2kπ± ,k∈Z
,k∈Z又
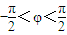 ,对k赋值知,∅=-
,对k赋值知,∅=-
故f(x)=sin(2x-
 )
)令f(x)=sin(2x-
 )=0
)=0可得2x-
 =kπ,k∈Z
=kπ,k∈Z故有x=
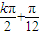 ,k∈Z,即对称中心的坐标是(
,k∈Z,即对称中心的坐标是( ,0)
,0)当k=0时,可知f(x)的图象关于点
 对称.
对称.故

点评:本题考点是由y=Asin(ωx+φ)的部分图象确定其解析式,在新教材的高考中,这种开放式答案不唯一的题近几年有增多的趋势.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
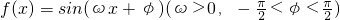 ,给出下列三个论断:
,给出下列三个论断: 对称;
对称;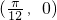 对称.
对称.