题目内容
对于定义域为D的函数f(x),若存在区间M=[a,b]⊆D(a<b),使得{y|y=f(x),x∈M}=M,则称区间M为函数f(x)的“等值区间”.给出下列三个函数:①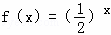 ; ②f(x)=x3; ③f(x)=log2x+1
; ②f(x)=x3; ③f(x)=log2x+1
则存在“等值区间”的函数的个数是 .
解答:解:①对于函数 ,若存在“等值区间”[a,b],由于函数是定义域内的减函数,故有
,若存在“等值区间”[a,b],由于函数是定义域内的减函数,故有 =a,
=a, =b,即(a,b),(b,a)点均在函数图象上,且两点关于y=x对称,两点只能同时是函数
=b,即(a,b),(b,a)点均在函数图象上,且两点关于y=x对称,两点只能同时是函数 ,与函数
,与函数 图象的唯一交点.即只能是a=b,故①不存在“等值区间”.②对于函数f(x)=x3存在“等值区间”,如 x∈[0,1]时,f(x)=x3∈[0,1].③对于 f(x)=log2x+1,由于函数是定义域内的增函数,故在区间[1,2]上有f(1)=1,f(2)=2,所以函数存在“等值区间”[1,2].存在“等值区间”的函数的个数是2个
图象的唯一交点.即只能是a=b,故①不存在“等值区间”.②对于函数f(x)=x3存在“等值区间”,如 x∈[0,1]时,f(x)=x3∈[0,1].③对于 f(x)=log2x+1,由于函数是定义域内的增函数,故在区间[1,2]上有f(1)=1,f(2)=2,所以函数存在“等值区间”[1,2].存在“等值区间”的函数的个数是2个

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
设f(x)是定义在R上的偶函数,且f(2+x)=f(2﹣x),当x∈[﹣2,0)时,f(x)=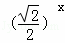 ﹣1,若在区间(﹣2,6)内的关于x的方程f(x)﹣loga(x+2)=0(a>0且a≠1)恰有4个不同的实数根,则实数a的取值范围是( )
﹣1,若在区间(﹣2,6)内的关于x的方程f(x)﹣loga(x+2)=0(a>0且a≠1)恰有4个不同的实数根,则实数a的取值范围是( )
|
| A. | ( | B. | (1,4) | C. | (1,8) | D. | (8,+∞) |
函数 (0<a<1)的图象的大致形状是( )
(0<a<1)的图象的大致形状是( )
|
| A. |
| B. |
| C. |
| D. |
|
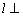 平面
平面 ,直线
,直线 平面
平面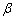 ,有下列四个命题:①若
,有下列四个命题:①若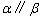 ,则
,则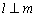 ;
;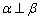 ,则
,则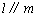 ;③若
;③若 且
且 ,求
,求 的值.
的值. ,1)
,1)



 ,
, B.
B.
 D.
D.
 ,若对于任意的
,若对于任意的 ,都有
,都有 满足方程
满足方程 ,这时
,这时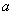 的取值集合为( )
的取值集合为( ) B.
B. C .
C . D.
D. 
 、
、 分别是定义在R上的奇函数和偶函数,当x<0时
分别是定义在R上的奇函数和偶函数,当x<0时 且
且 ,则不等式
,则不等式 的解集为
的解集为