题目内容
 下列关于星星的图案构成一个数列{an},an(n∈N*)对应图中星星的个数
下列关于星星的图案构成一个数列{an},an(n∈N*)对应图中星星的个数(1)写出a5,a6的值及数列{an}的通项公式;
(2)求出数列{
| 1 |
| an |
(3)若bn=
| 2n2-9n-11 |
| 2n |
分析:(1)由图中所给的星星个数:1,1+2,1+2+3,…,1+2+3+…+n;得出数列第n项,即通项公式.
(2)由an=
,知
=2(
-
),利用裂项求和法能求出{
}的前n项和Sn.
(3)由bn=
,Sn=
,知cn=Sn•bn=
×
=2n-11,由此能求出数列{|cn|}的前n项和.
(2)由an=
| n(n+1) |
| 2 |
| 1 |
| an |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| an |
(3)由bn=
| 2n2-9n-11 |
| 2n |
| 2n |
| n+1 |
| 2n |
| n+1 |
| 2n2-9n-11 |
| 2n |
解答:解:(1)从图中可观察星星的构成规律,
n=1时,有1个;
n=2时,有1+2=3个;
n=3时,有1+2+3=6个;
n=4时,有1+2+3+4=10个;
∴a5=1+2+3+4+5=15,
a6=1+2+3+4+5+6=21.
an=1+2+3+4+…+n=
.
(2)∵an=
,
∴
=
=2(
-
),
∴{
}的前n项和Sn=2[(1-
)+(
-
)+…+(
-
)]=2(1-
)=
.
(3)∵bn=
,Sn=
,
∴cn=Sn•bn=
×
=2n-11,
∴数列{|cn|}的前n项和:
Tn=|2-11|+|4-11|+|6-11|+|8-11|+|10-11|+|12-11|+|14-11|+…+|2n-11|
=9+7+5+3+1+1+3+…+(2n-11)
=-a1-a2-a3-a4-a5+a6+a7+…+an
=
=
=
.
n=1时,有1个;
n=2时,有1+2=3个;
n=3时,有1+2+3=6个;
n=4时,有1+2+3+4=10个;
∴a5=1+2+3+4+5=15,
a6=1+2+3+4+5+6=21.
an=1+2+3+4+…+n=
| n(n+1) |
| 2 |
(2)∵an=
| n(n+1) |
| 2 |
∴
| 1 |
| an |
| 2 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
∴{
| 1 |
| an |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n+1 |
| 2n |
| n+1 |
(3)∵bn=
| 2n2-9n-11 |
| 2n |
| 2n |
| n+1 |
∴cn=Sn•bn=
| 2n |
| n+1 |
| 2n2-9n-11 |
| 2n |
∴数列{|cn|}的前n项和:
Tn=|2-11|+|4-11|+|6-11|+|8-11|+|10-11|+|12-11|+|14-11|+…+|2n-11|
=9+7+5+3+1+1+3+…+(2n-11)
=-a1-a2-a3-a4-a5+a6+a7+…+an
=
|
=
|
=
|
点评:本题考查数列的通项公式和前n项和公式的求法,解题时要认真审题,仔细解答,注意观察法、裂项求和法、分类讨论法的灵活运用.

练习册系列答案
相关题目
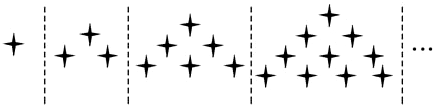
下列关于星星的图案构成一个数列,该数列的一个通项公式是( )

| A、an=n2-n+1 | ||
B、an=
| ||
C、an=
| ||
D、an=
|
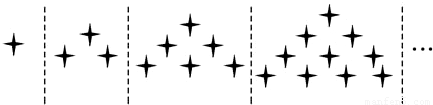
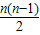
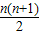
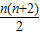
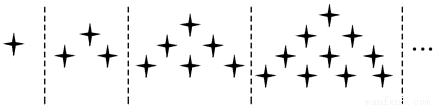
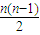
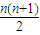
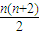
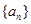 ,
,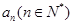 对应图中星星的个数.
对应图中星星的个数.
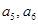 的值及数列
的值及数列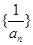 的前n项和
的前n项和 ;
;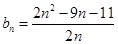 ,对于(2)中的
,对于(2)中的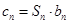 ,求数列
,求数列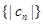 的前n项和
的前n项和 ;
;