题目内容
【题目】（Ⅰ）函数f（x）满足对任意的实数x，y都有f（xy）=f（x）+f（y），且f（4）=2，求f（ 
）的值； （Ⅱ）已知函数f（x）是定义在[﹣1，1]上的奇函数，且f（x）在[﹣1，1]上递增，求不等式f（x+ 
）+f（x﹣1）＜0
的解集．
【答案】解：（Ⅰ）f（4）=f（2×2）=f（2）+f（2）=2 ∴2f（2）=2f（2）=1
又∵f（2）=f（ 
）=f（ 
）+f（ ）═
∴2f（ ）=1f（ ）= 
（Ⅱ）由f（x）是[﹣1，1]上的奇函数得f（x+ ）＜f（1﹣x）
又f（x）在[﹣1，1]上递增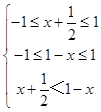
解得 
∴不等式解集为[0， 
）
【解析】解：（Ⅰ）直接利用赋值法求得（Ⅱ）由f（x）是[﹣1，1]上的奇函数得f（x+ 
）＜f（1﹣x），又f（x）在[﹣1，1]上递增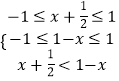 
练习册系列答案
相关题目
